学习了李宏毅教授的2019年及2021年ML课程后所做的笔记,暂未包括助教的内容和作业内容,目的是快速的过一遍课程,所以有些地方笔记也不详细,之后有需要再去看吧~;
老师的个人主页网址:https://speech.ee.ntu.edu.tw/~hylee/index.html,课程资料可以在这里找到。
- Introduction
- Deep Learning
- Convolutional Neural Network
- Self-Attention
- Transformer
- Generative Model
- Self-supervised Learning
- Adversarial Attack
- Explainable AI
Introduction
Introduction (slide), Rule (slide)
机器学习就是找函数,根据输入,希望得到一定输出
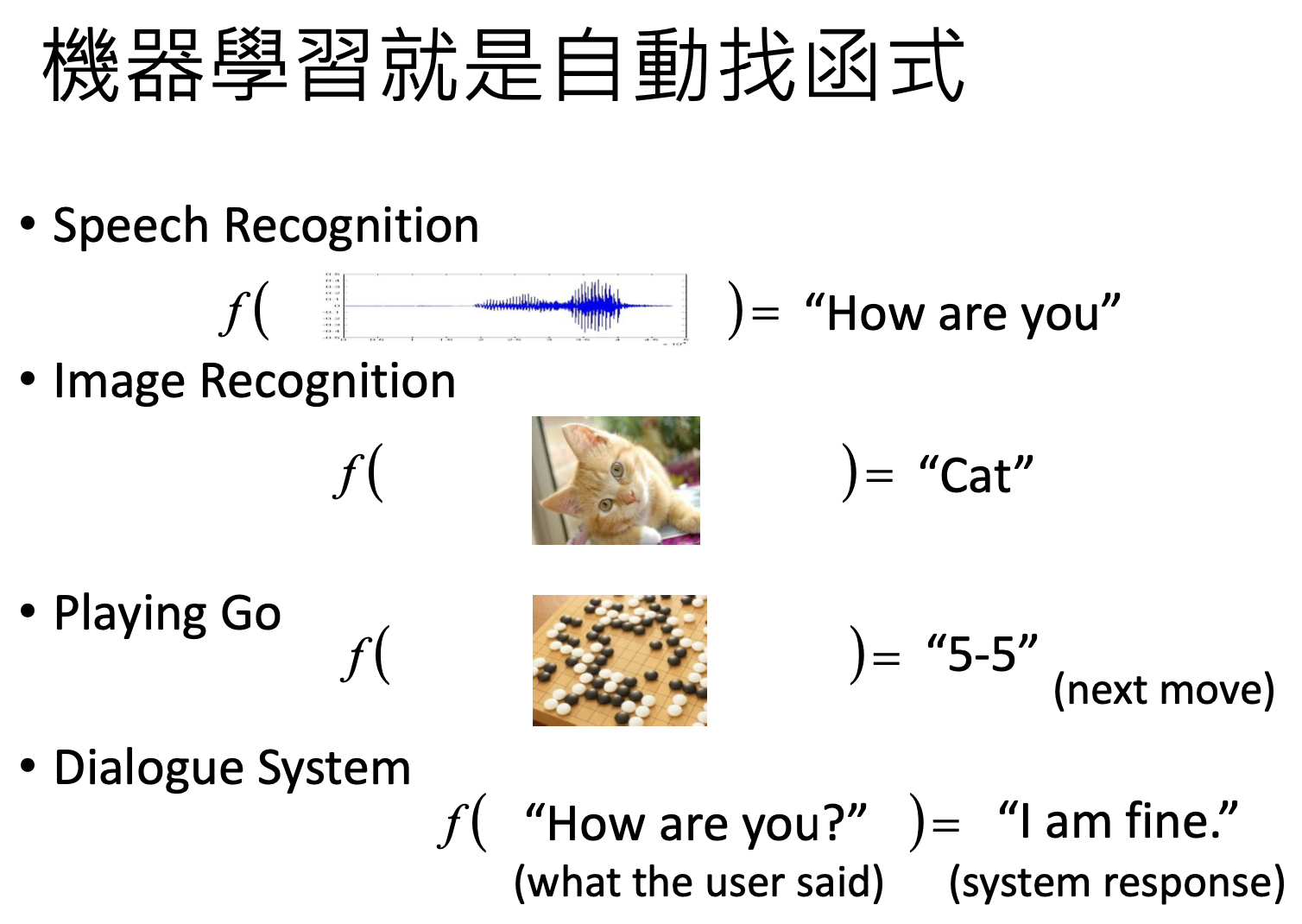
根据期望的不同的函数,ML可以分为Regression,Classification,Generation 。
其中Generation (生成),即产生有结构的负责东西 (例如:文句、图片)。
机器学习可以分为三个步骤
- 设立Function Set,即构建神经网络模型
- 规定如何判断Function好坏
- 在Function Set中寻找最优的Function
Deep Learning
Regression
不同的model代表了不同的function set,根据data我们最终会从function set中选出最合适的function。
如果是尝试minimize一个function,这个function称为loss function,如果是尝试maximize一个function,这个function称为object function。
训练过程中,loss function定义了model的好坏,loss function是function (Model) 的function。
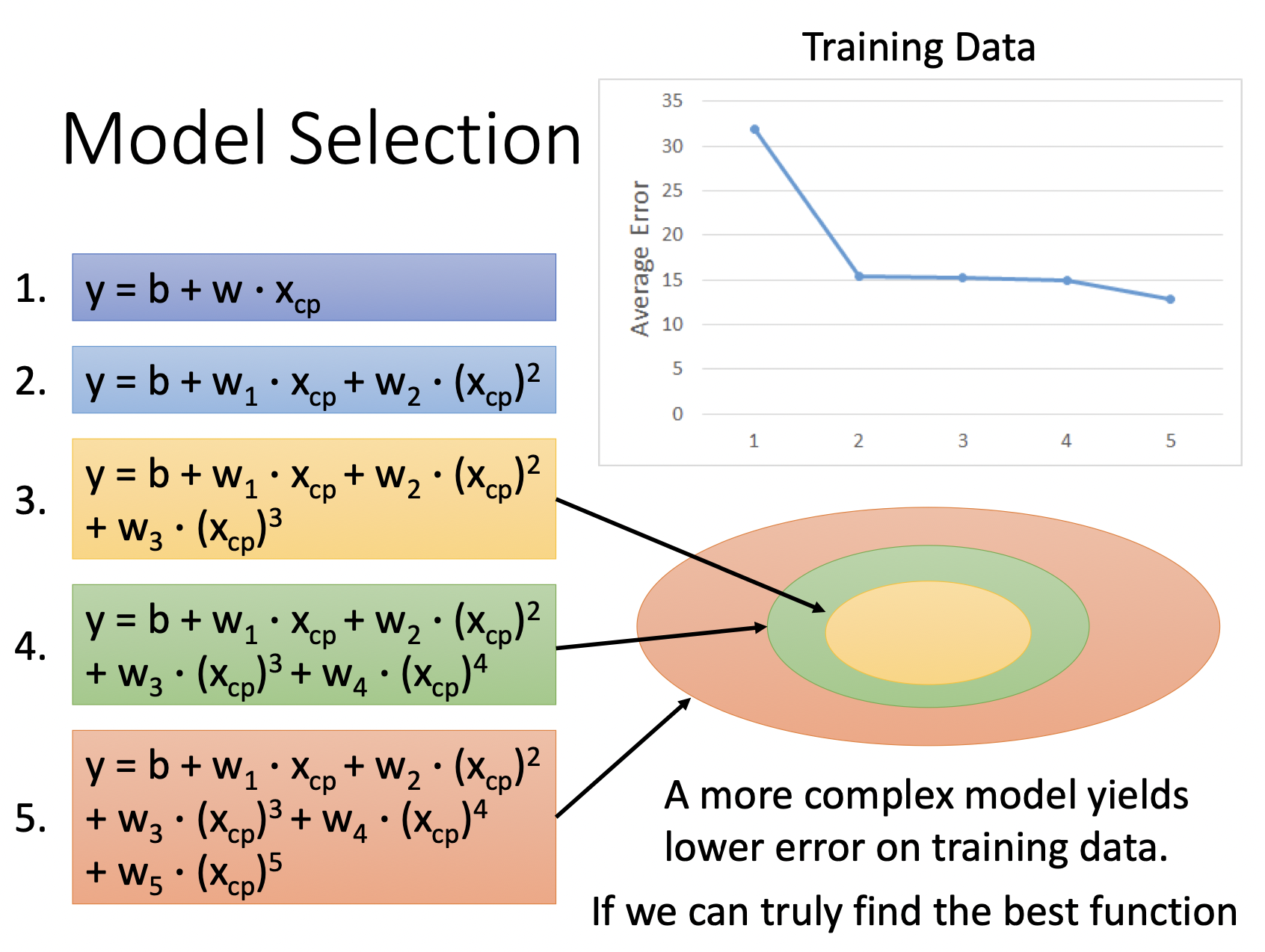
更复杂的model代表着更大的function set,更有可能包括着best function,但更复杂的model可能过拟合training data的分布,而在test data 上没有好表现。

Regularization将loss function添加了一项term,代表我们希望更smooth的function,越平滑的function对输入越不敏感。
Where does the error come from?
error来自bias (均值) 以及variance (方差)
实际实验中的方差通常比真实值方差要小,他们之间的比值如下
\[E(s^2) = \frac{N-1}{N} \sigma^2\]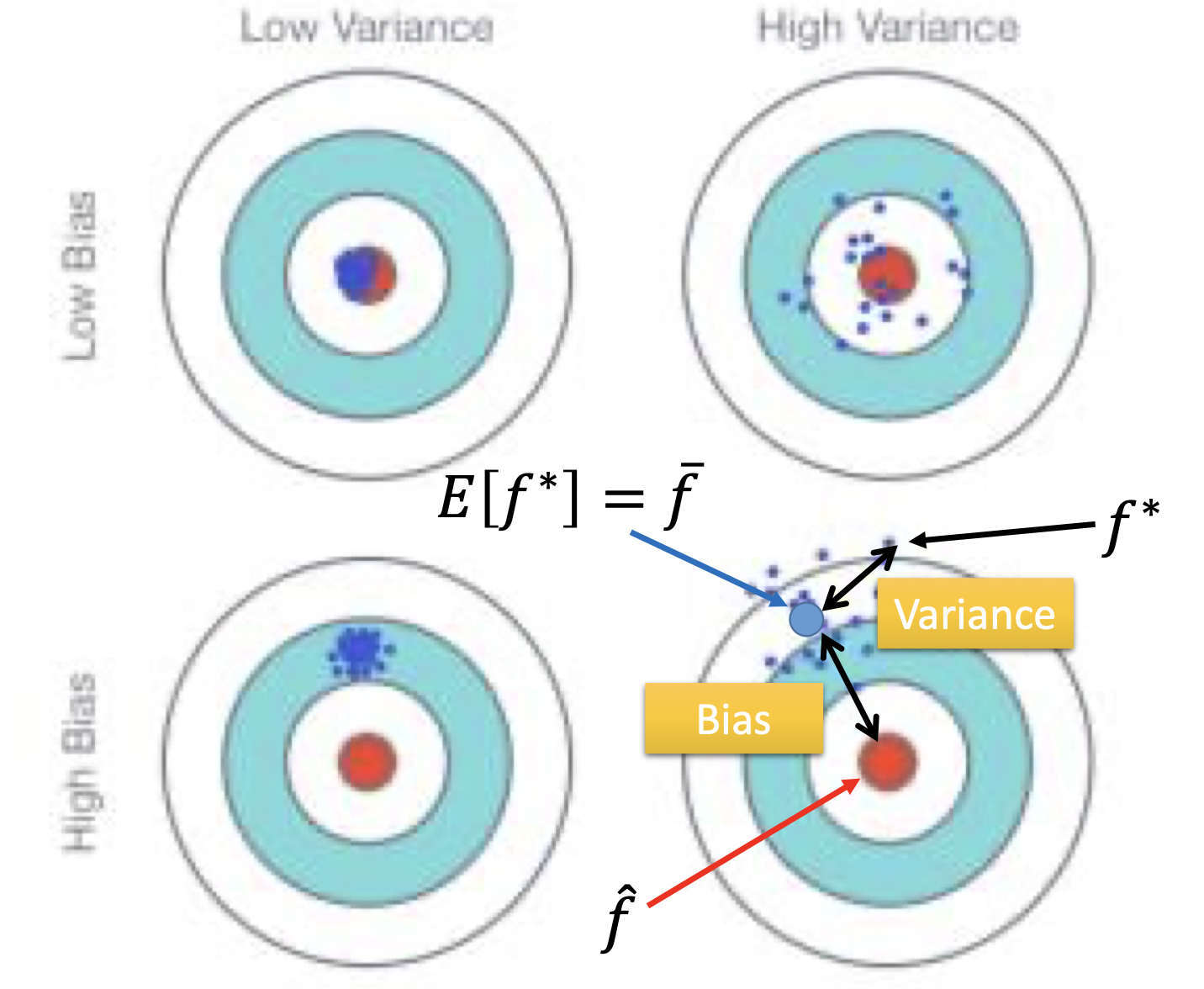
bias大,对应underfitting,应该调整模型结构,例如增加feature,因为也许你现在的function set没有包含正确的target function,variance大,对应overfitting,可以选择增加数据 (不会影响bias),或者Regularization (强制模型smooth,伤害bias)。
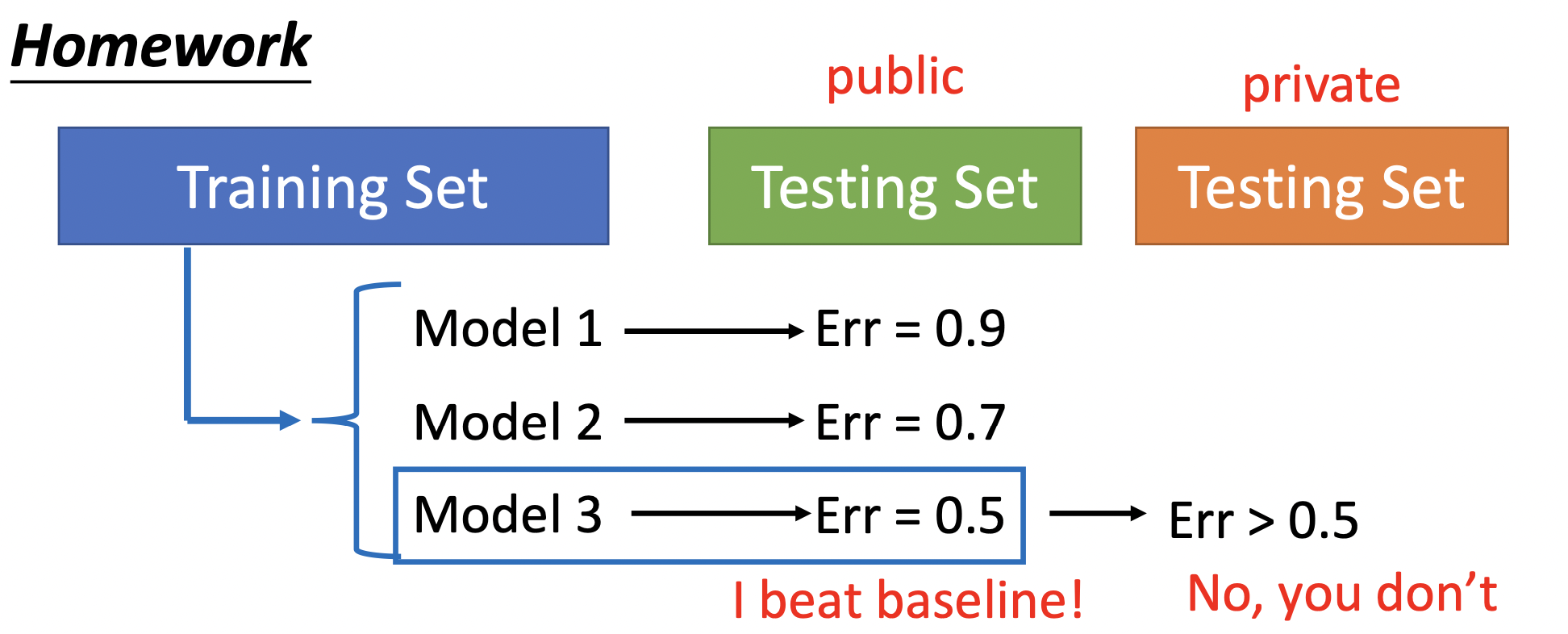
假设从Training set中学到了三个不同的model,Model 1 2 3,这些model是努力拟合Training set的结果,根据他们在public Testing Set中的表现,选择public Testing Set上Err最低的一个,此Model不仅拟合Training set,而且最好的拟合了public Testing Set,也许他最接近拟合“真实数据”。但是此Model在private Testing Set上的表现是未知的,因为private Testing Set又有自己的数据分布。
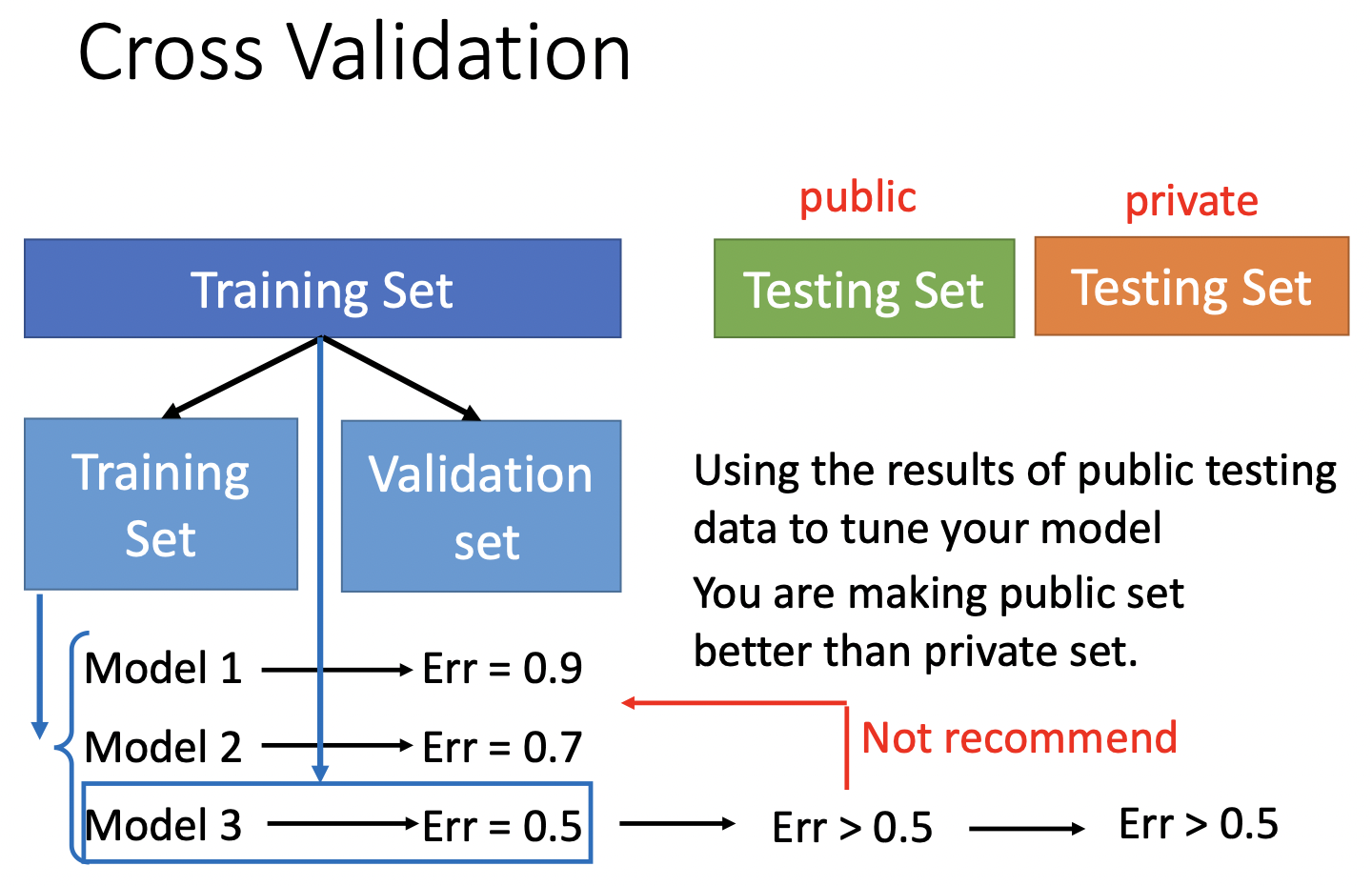
一种方法是Cross Validation (交叉验证),把原Training Set分为Training Set与Validation set两部分,用Training Set训练,选出Validation set Err最小的那个,再用整一个(Training Set + Validation set)训练一遍,这时候public Testing Set上的Err才能反应private Testing Set上的error。如果不信任分一次的结果,就分好多次,即N-fold Cross Validation(N折交叉验证)。
Gradient Descent
Gradient Descent 1 2 3 (slide)
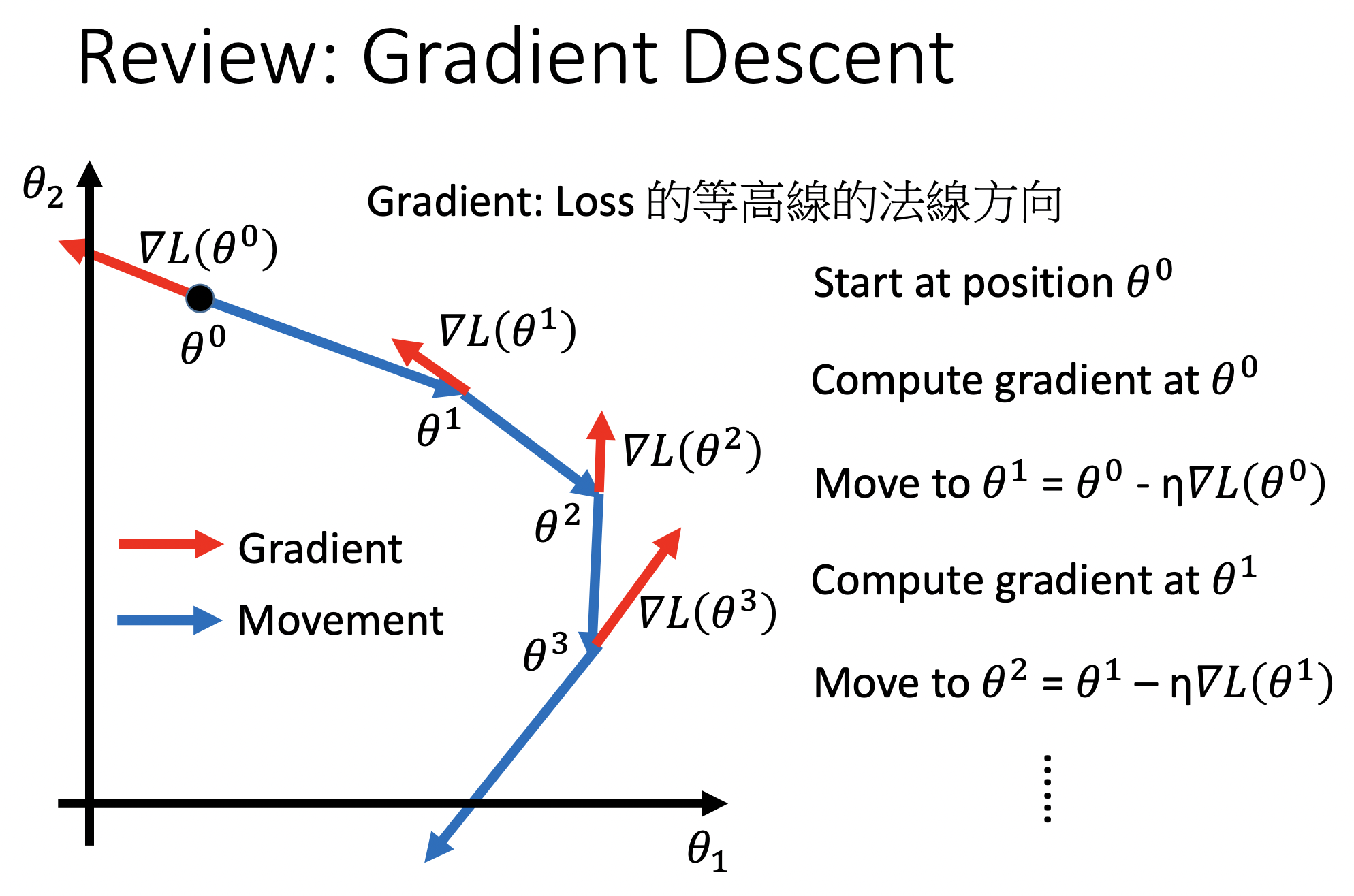
用倒三角表示梯度
\[\nabla L(\theta ) = \begin{bmatrix} \frac{\partial L(\theta_1 )}{\partial \theta_1} \\ \frac{\partial L(\theta_2 )}{\partial \theta_2} \end{bmatrix}\]Gradient Descent (梯度下降法)使$\theta$向梯度反方向移动一定长度,其中一个重要参数是$\eta $,称为learning rate,lr。
$\eta$的大小需要设计,可以画出lr-loss图,找到适合的lr。
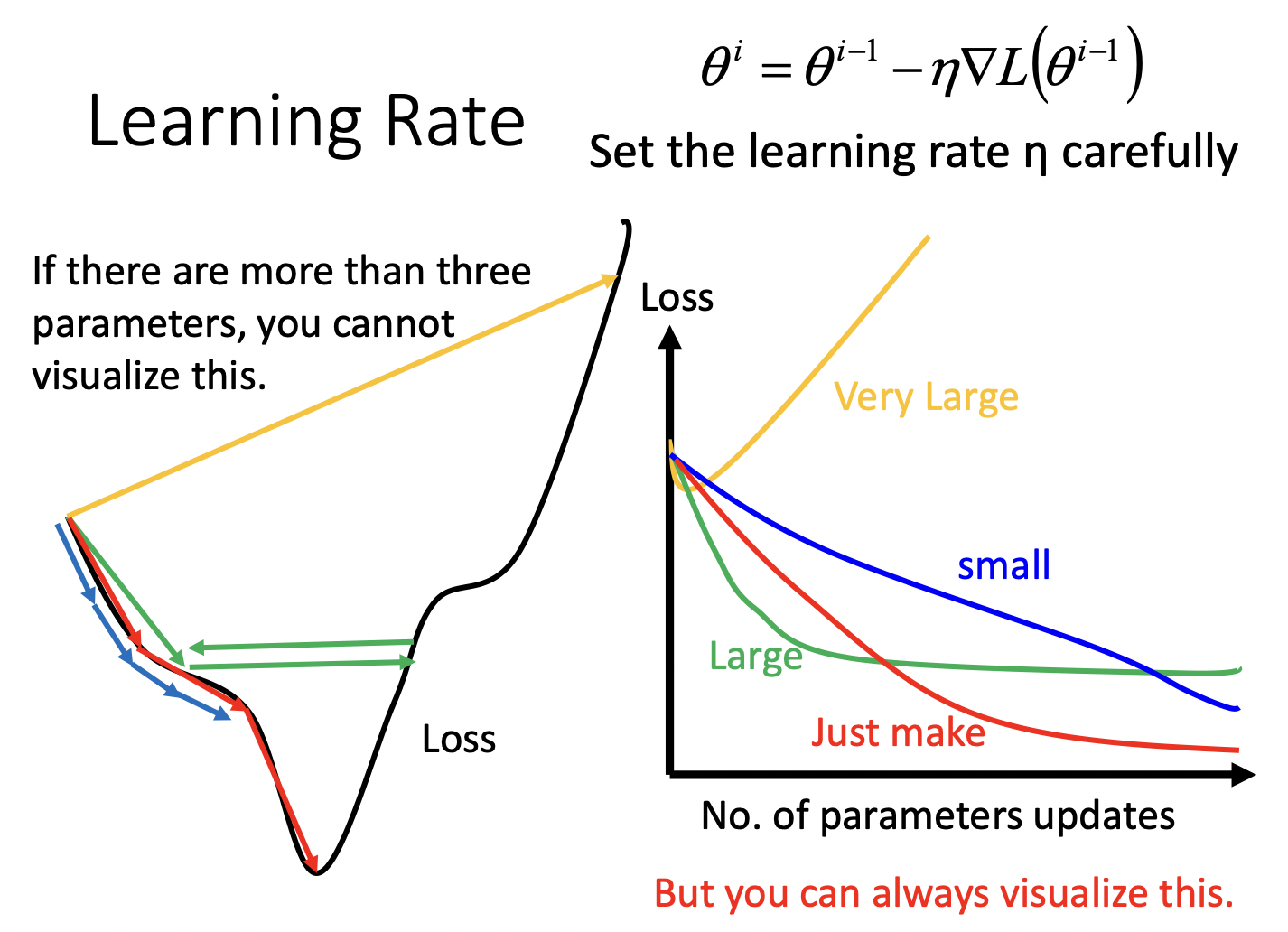
有一些自动调整lr的方法,其中的大原则是:一般认为刚开始训练的时候,离最低点较远,所以刚开始lr应较大,随着参数的update,越来越接近最低点,lr应该越来越小。
Adagrad
Adagrad对$\theta $中的每个参数$w$生成单独的lr

其中$\sigma^t$代表$w$的前$t$时刻导数$g$的均方根
\[\sigma^t = \sqrt{\frac{1}{t+1} \sum^t_{i=0} (g^i)^2}\]$w$的更新式子上下经都有$\sqrt{t+1}$,整理可得
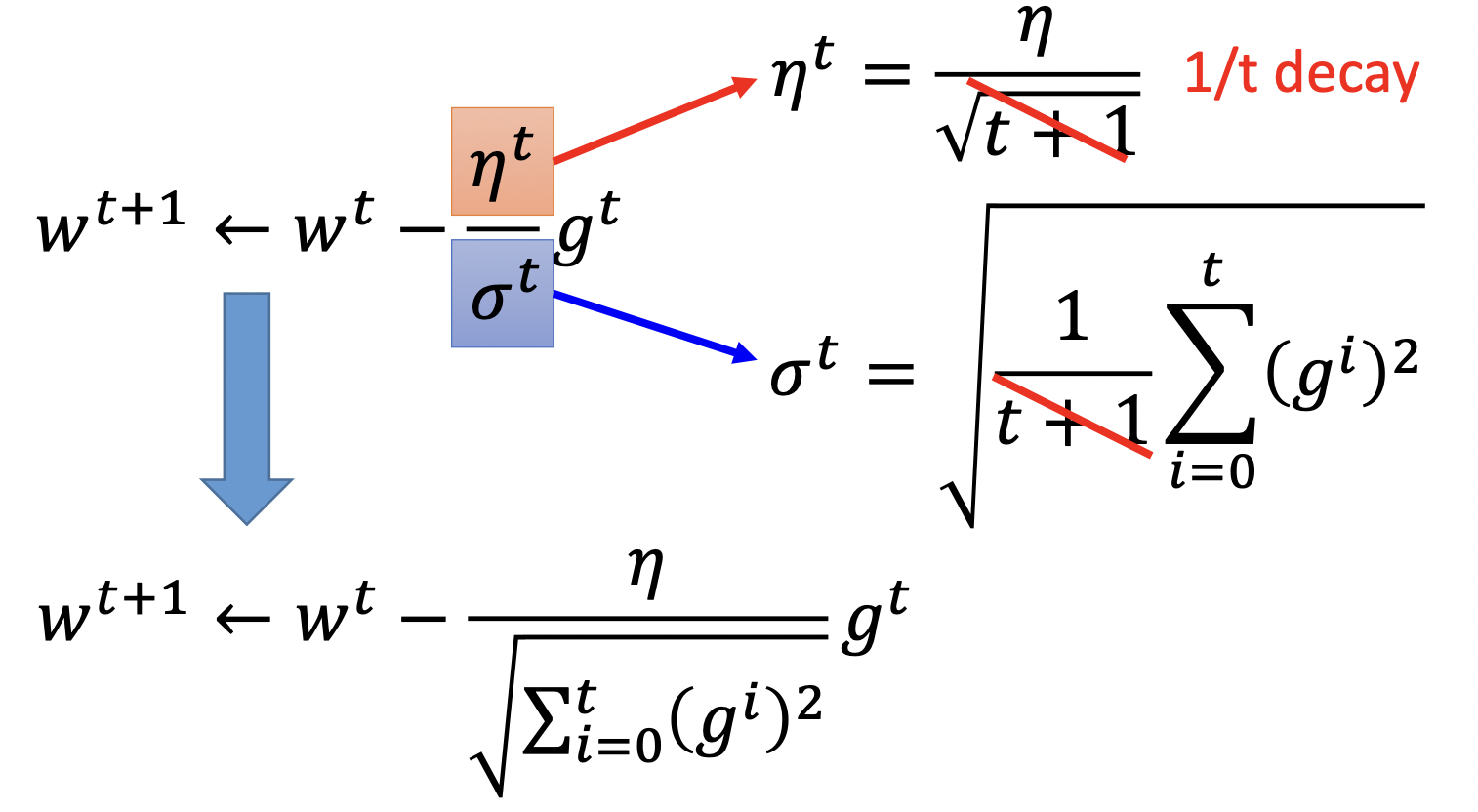
看起来也许有些奇怪,标红和标蓝的部分朝相反的方向努力:红色部分告诉我们$g^t$越大步越大,蓝色部分告诉我们$g^t$越大步越小。
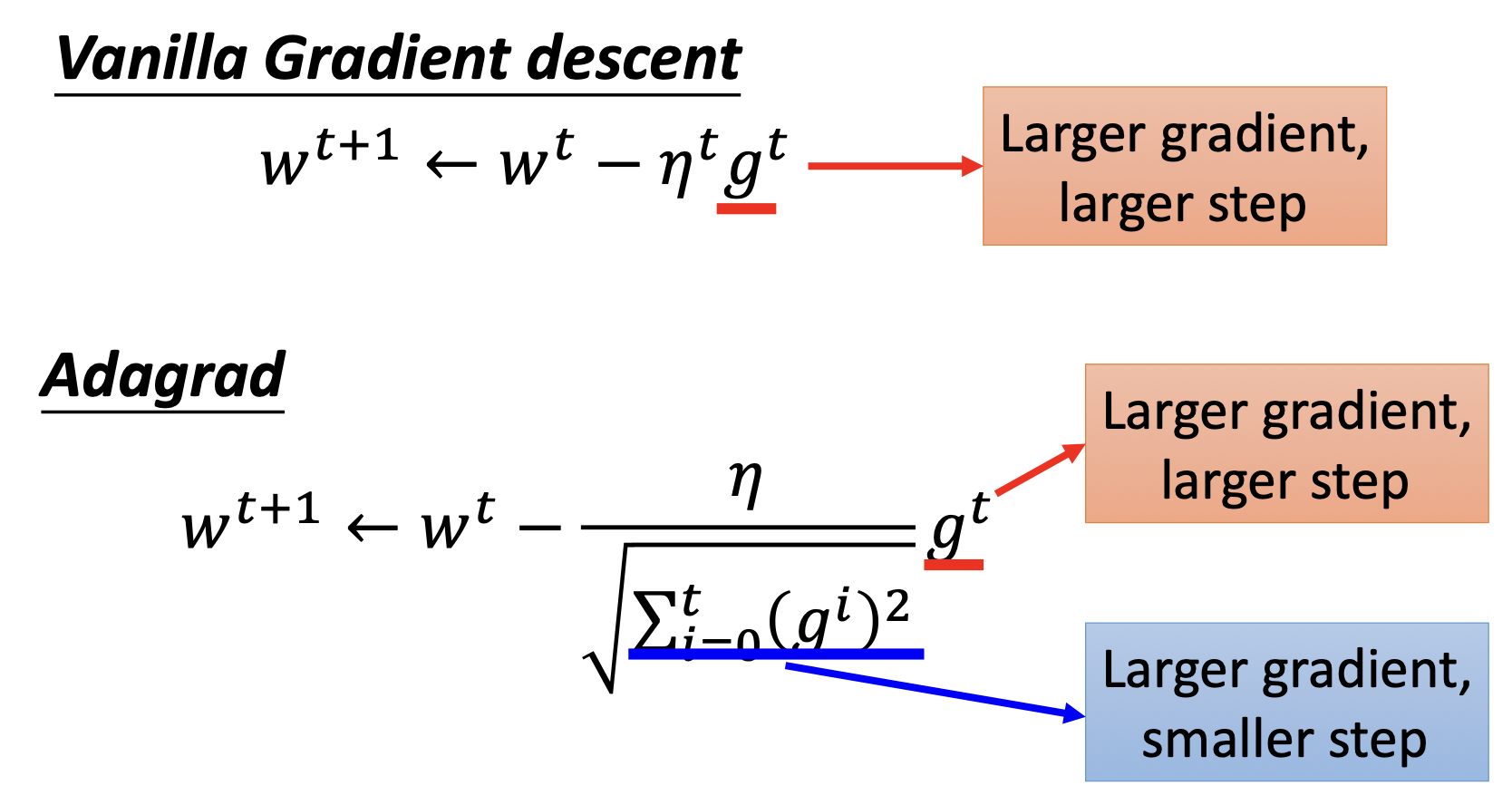
一种解释是这种安排造成了一种反差的效果,显示此次更新与以前更新的差距

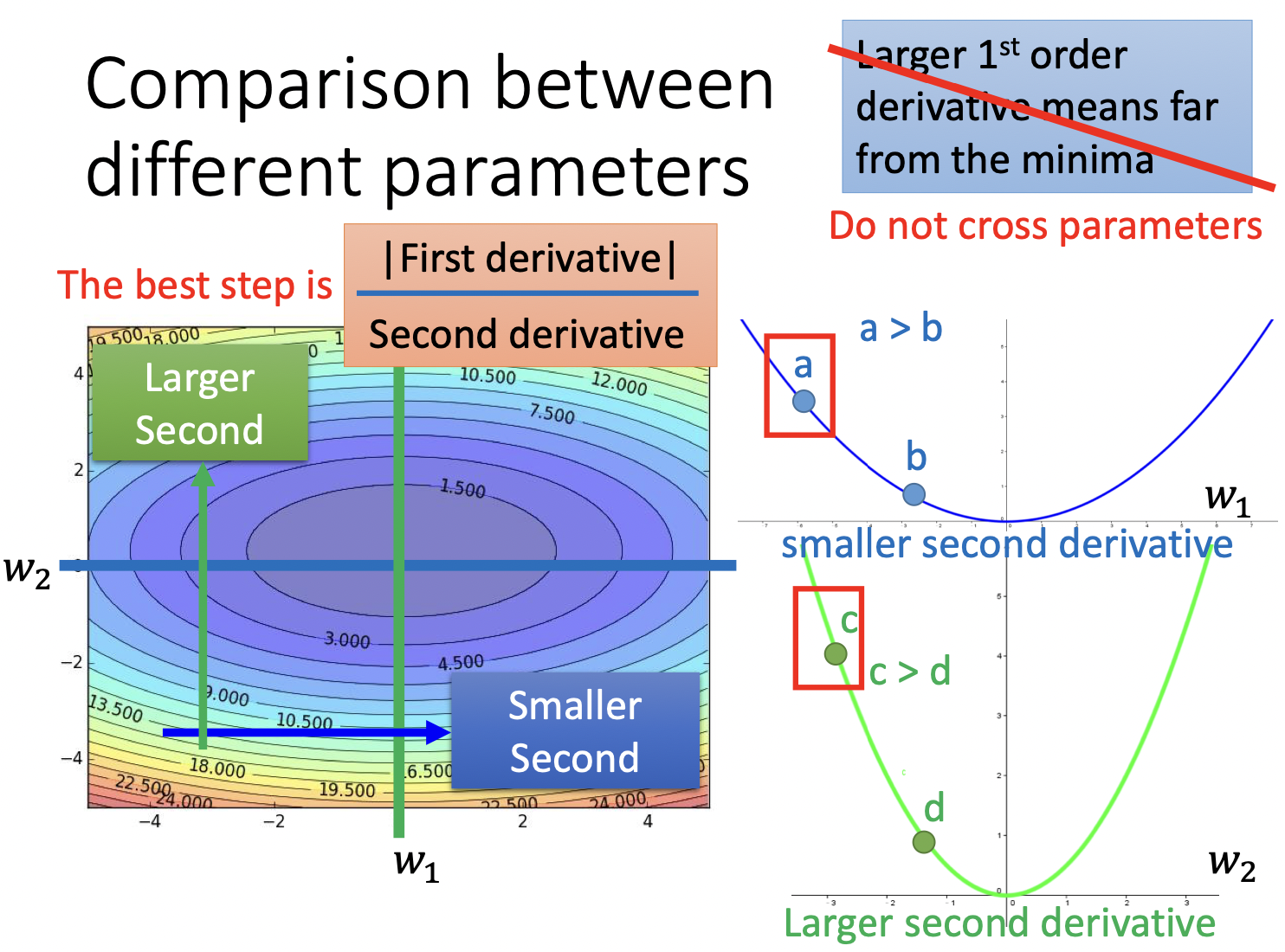
另一种解释是当有跨参数出现时,我们的步长不仅应该与一次微分成正比,还应该与二次微分成反比
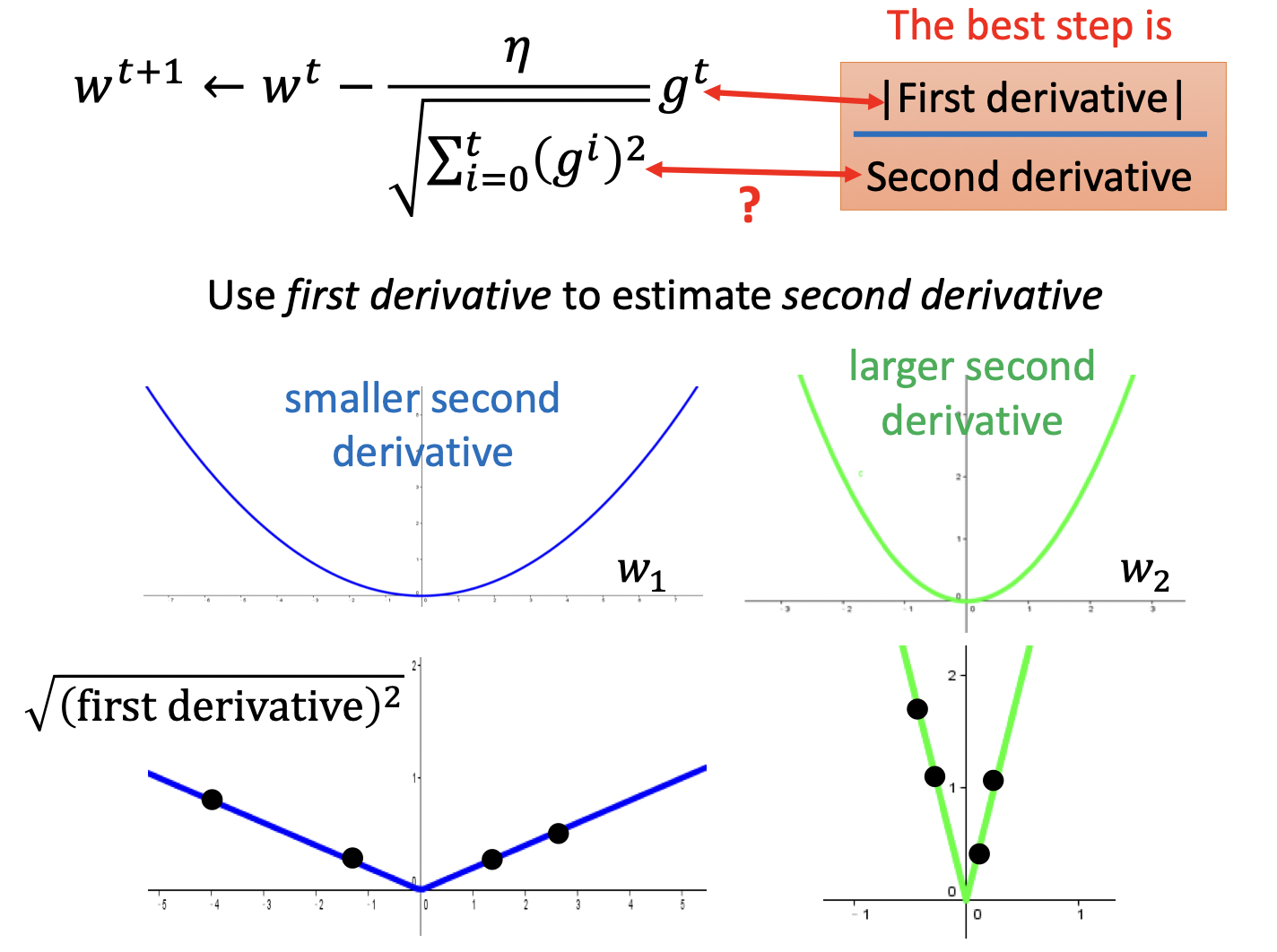
为了减少计算量,我们并不真正计算二次微分,而是用$\sqrt{\sum^t_{i=0} (g^i)^2}$近似
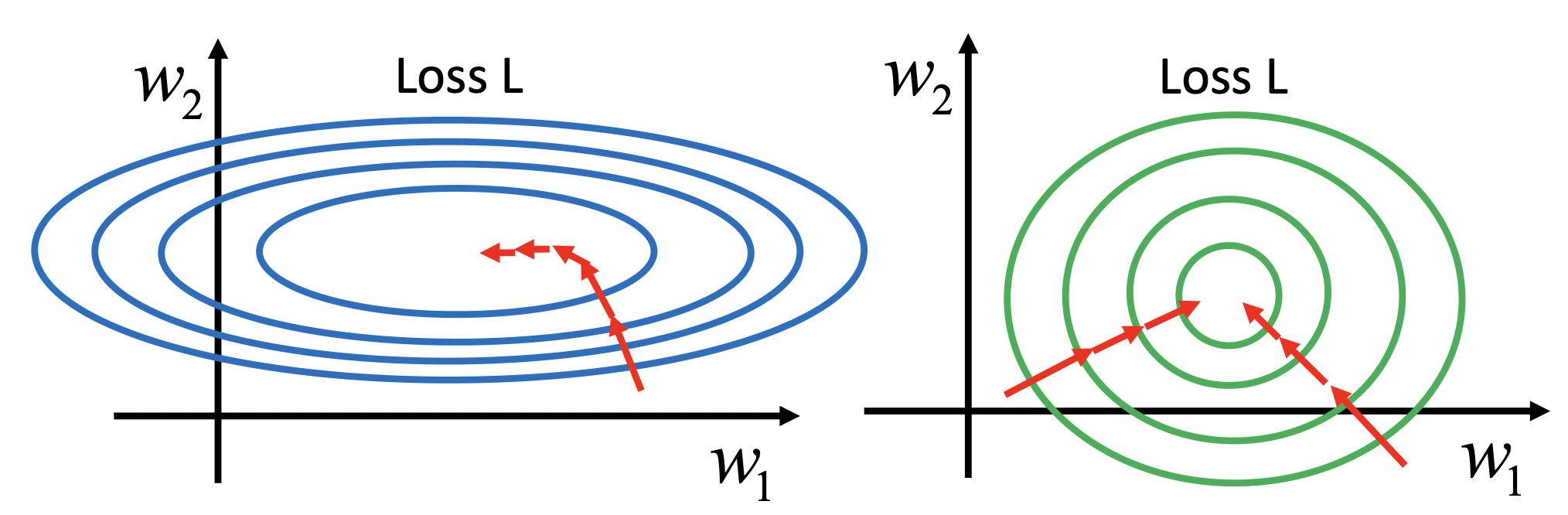
Feature Scaling
多维数据如果分布差距较大,梯度下降法一开始并不是指向最低点的 (如左侧图),建议做Scaling。
Classification
不应该使用Regression代替Classification,因为Regression会惩罚那些过于“正确的”数据
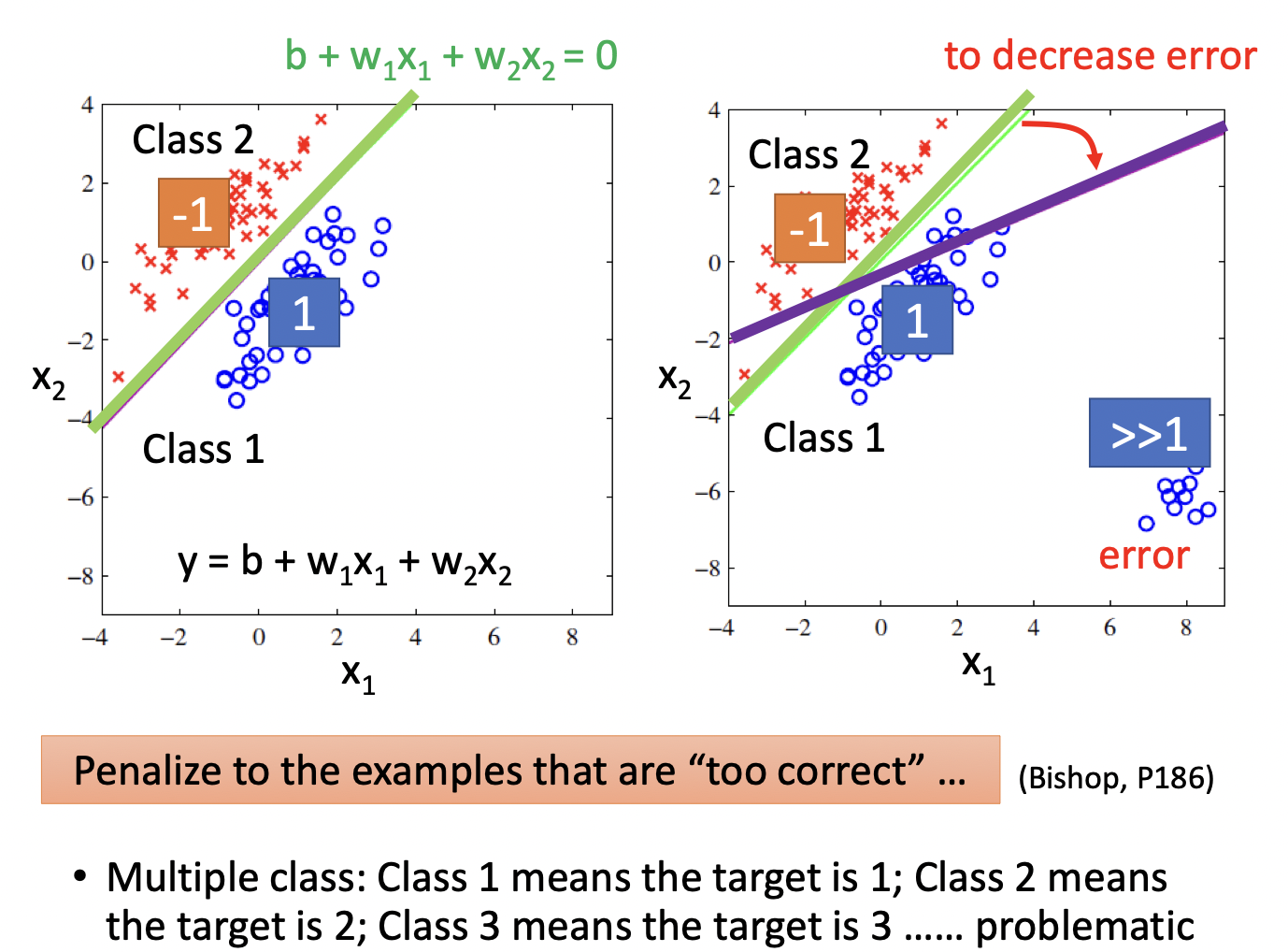
给定一个$x$,假定有两个类别$C_1,C_2$,$x$属于$c_1$的概率即为$\frac{x \text{属于类1的概率}}{x \text{属于类1的概率} + x \text{属于类2的概率}}$
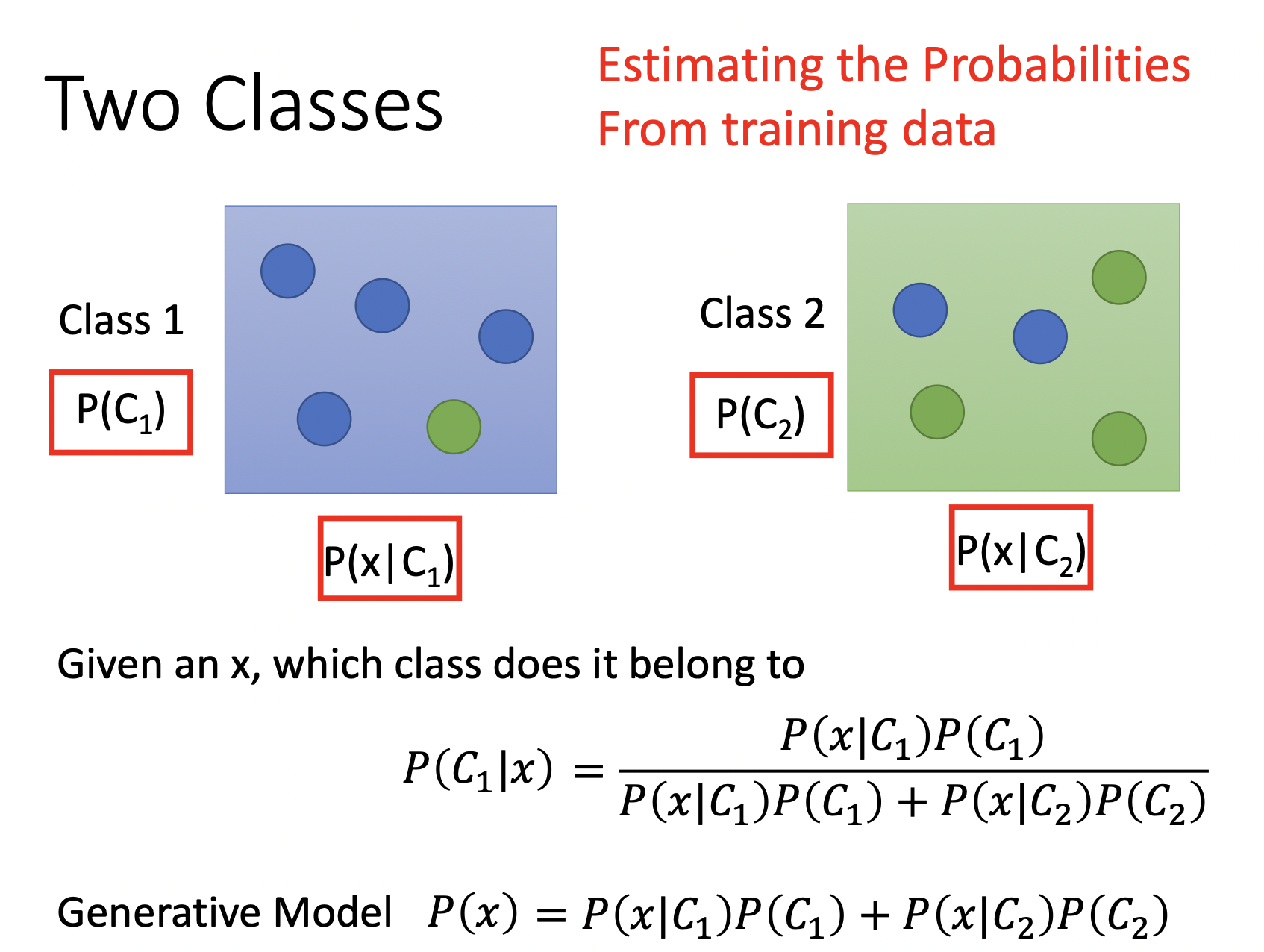
其中,$P(C_1),P(C_2)$都容易通过计算得到 ,如$\frac{C_1 \text{个数}}{C_1 \text{个数} + C_2 \text{个数}} $,但$P(x\mid C), P(x \mid C_2)$不能通过简单的计数算得,$x$可能并不包含在Training Set中,这种情况并不能简单的认为$x$属于某类的概率为0,我们需要以某种方式估算$P(x \mid C_1), P(x \mid C_2)$,即从类别$C_1, C_2$中抽样出$x$的概率。
这种模型又叫Generative Model,因为在这之后我们可以估计抽样出$x$的概率
回到上面说的估算问题,假设真实世界的数据是高斯分布的
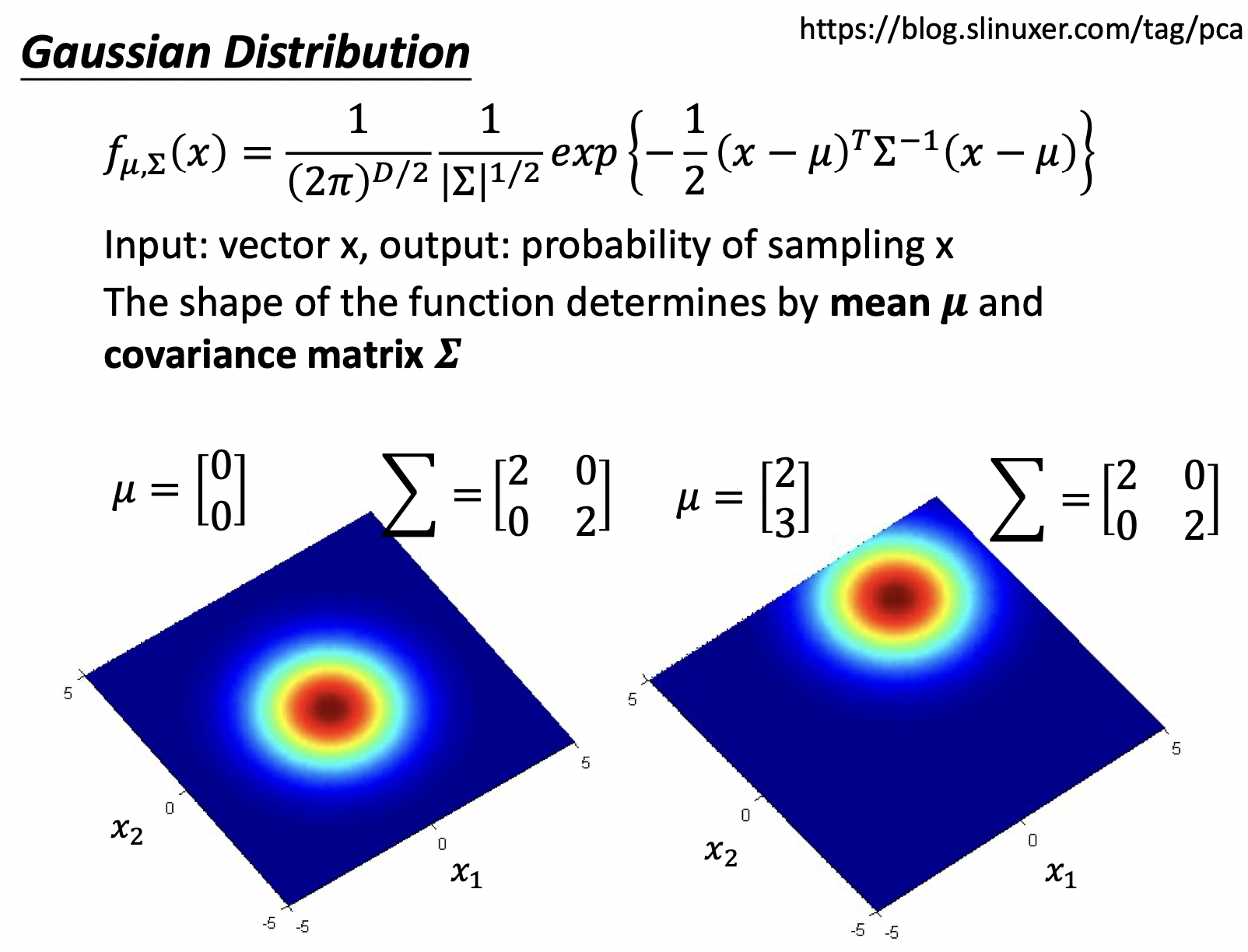
为了找到最接近真实数据分布的高斯分布,我们需要找到合适的均值$\mu$,协方差矩阵$\sum$,即根据此高斯分布,sample出目前的Training Set的可能性是最大的
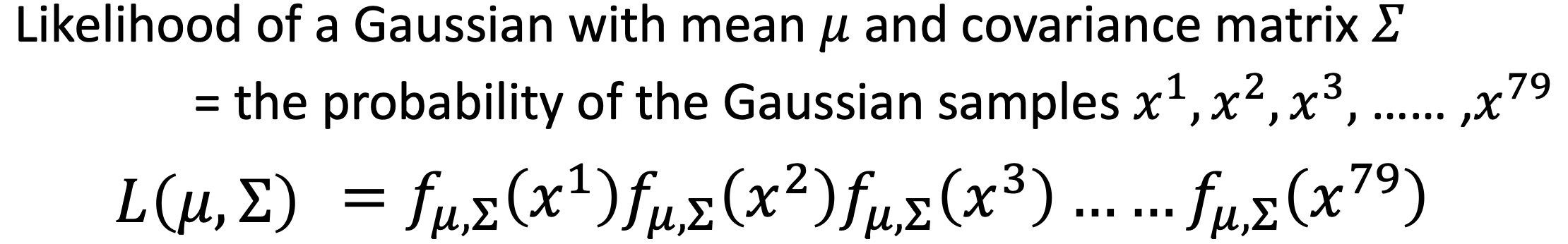
最后算出对应的$\mu$和$\sum$,得到合适的高斯分布,既可以计算$P(x\mid C), P(x \mid C_2)$,并计算$x$属于这些类的概率。
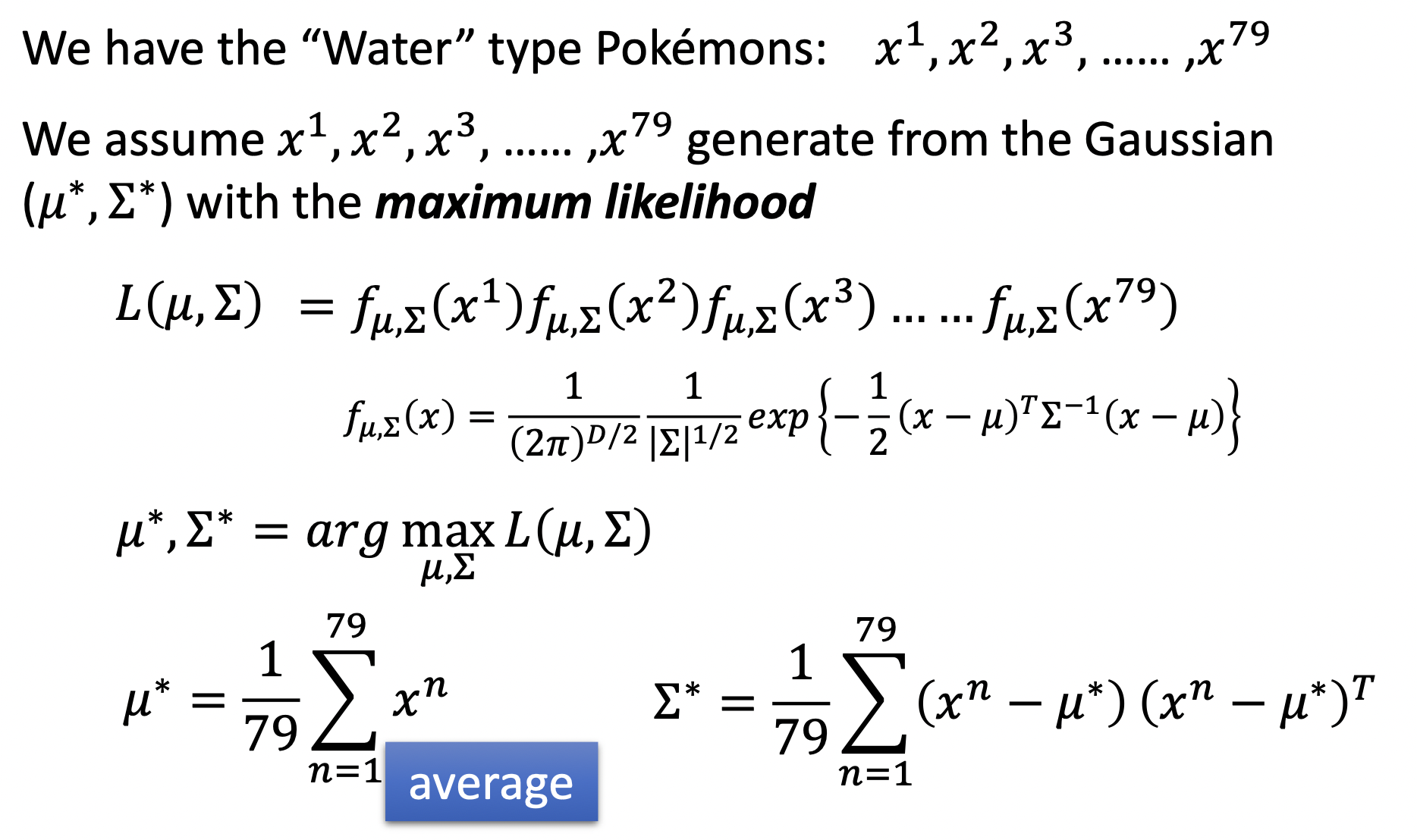
为了减少计算量,可以选择共用协方差矩阵,即只寻找$\mu_1, \mu_2, \sum$,计算可得$\sum$为$\sum_1,\sum_2$ weight by 各自种类element的数目。
除了Gaussian Distribution,另一种常见的Probability Distribution模型是Naive Bayes,即认为feature之间independent,$P(x \mid C)$可以看作是多个$1-D$ Gaussian机率的乘积。
\[P(x|C_1) = P(x|C_1)P(x_2|C_1) \dots P(x_k|C_1)\]对Posterior Probability (后验概率)的公式进行整理
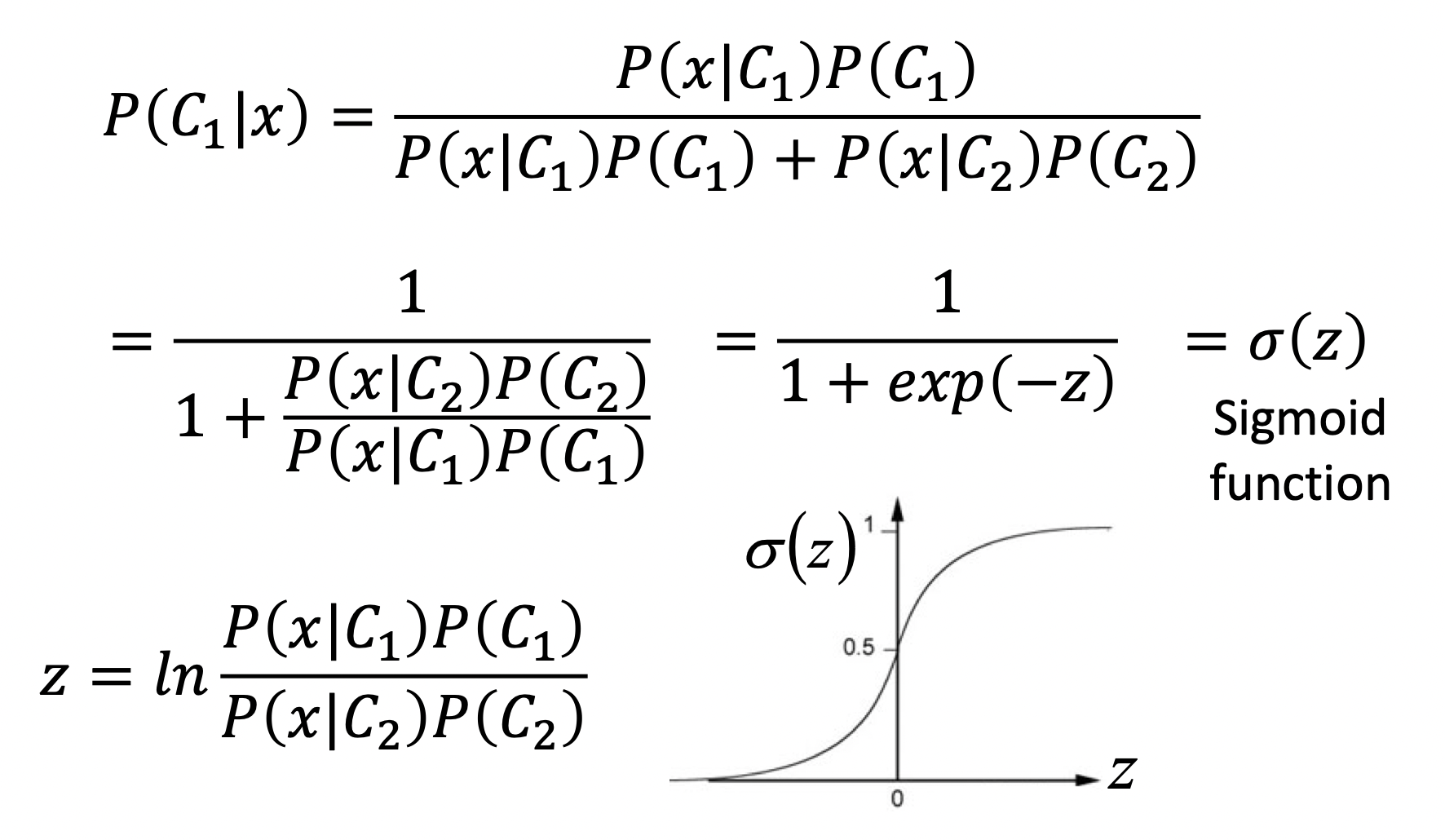
后验概率是关于$z = ln \frac{P(x \mid C_1)P(C_1)}{P(x \mid C_2) P(C_2)}$的Sigmoid function,经过计算可得$z$可以看作是$w\cdot x + b$的形式,即$P(C_1 \mid x) = \sigma (w\cdot x + b)$,在上面的Generative Model中,我们计算出了$N_1,N_2,\mu_1,\mu_2,\sum$,根据他们计算出$w,b$。
另一种方法是,我们直接尝试寻找$w,b$,并将$w\cdot x + b$投入Sigmoid function中,即Logistic Regression。
Logistic Regression
假设有一个二分类问题,想找到一个模型,输出$f_{w,b}(x) = P_{w,b}(C_1 \mid x) = \sigma(w \cdot x + b)$,当$P_{w,b} \ge 0.5$时,认为$x$属于$C_1$,否则属于$C_2$。Training Set中,$\hat{y} \in { 0, 1}$分别代表两个类别,即Bernoulli distribution。
最优的$w,b$应该满足,根据$w,b$抽样出Training Set的概率是最大的 ,$f_{w,b}$代表了属于$C_1$的概率,对应$C_2$类的概率就是$1-f_{w,b}$

对最大化取$-ln$,转为最小化,$ln$将乘积转为和。
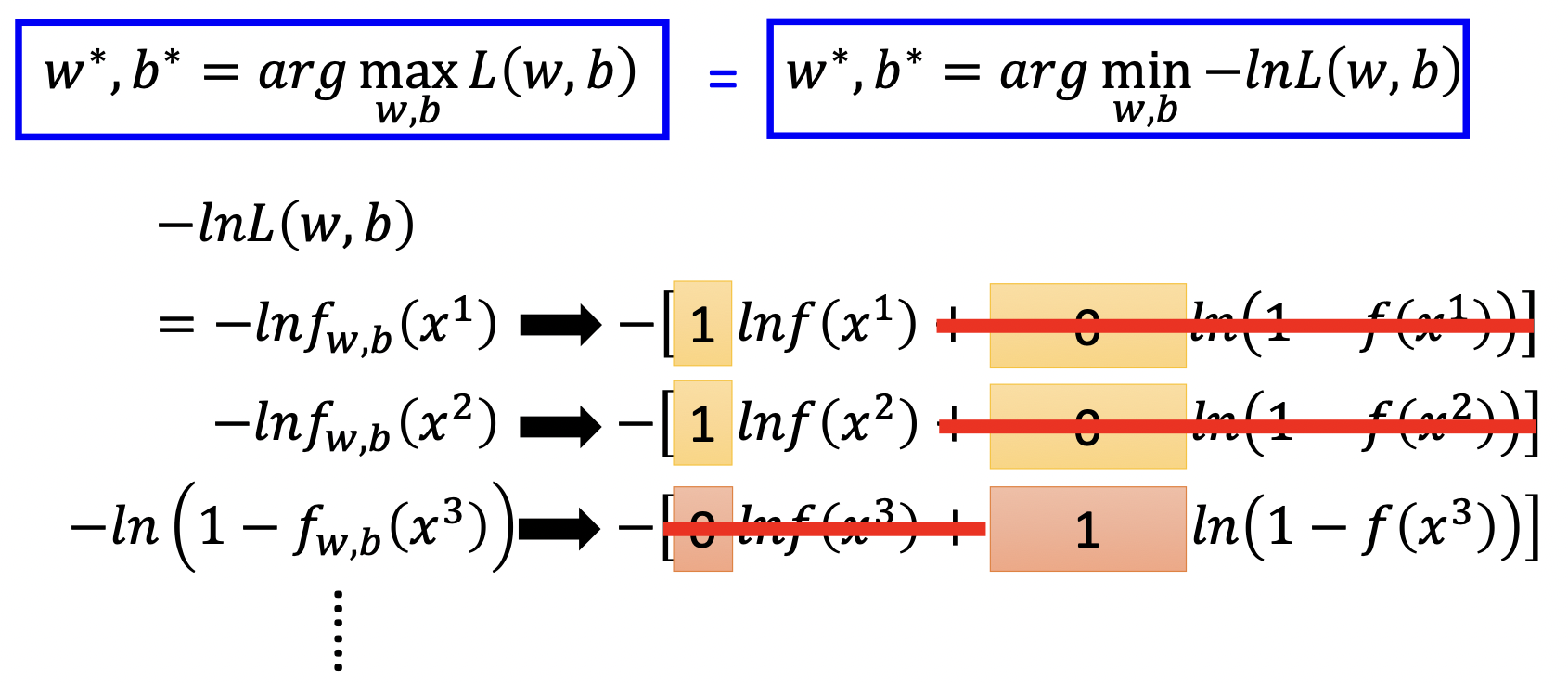
经过整理得到
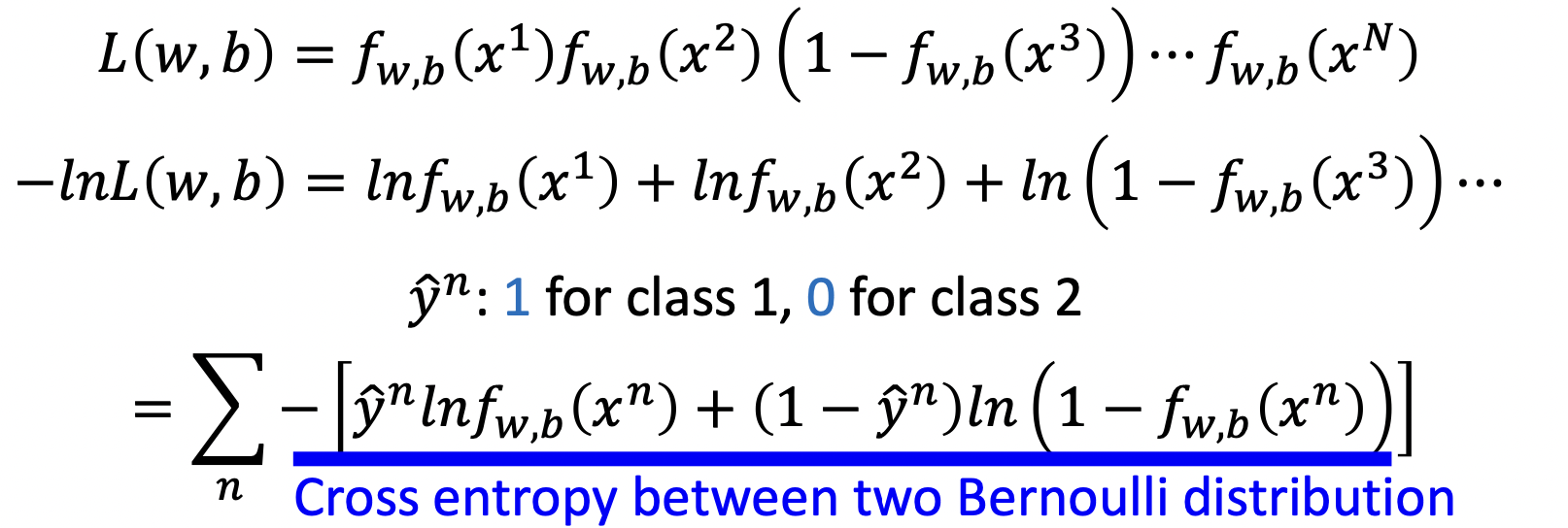
蓝线部分是两个伯努利分布 (一个是测量值的伯努利分布,一个是模型预测出来的伯努利分布) 的交叉墒,交叉墒计算公式如下
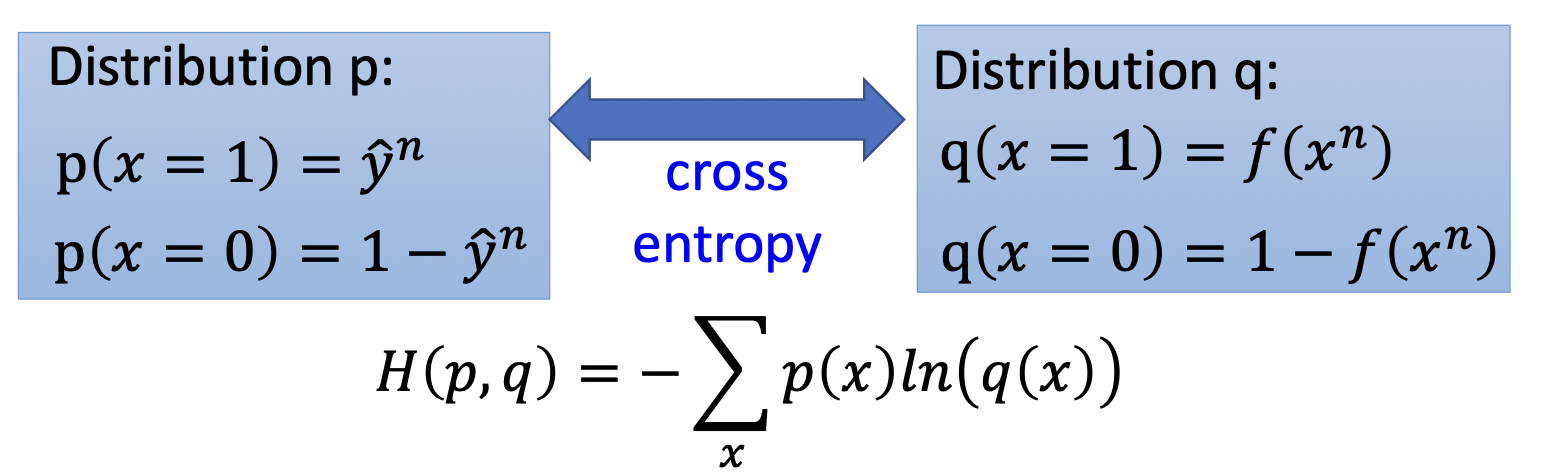
最终得到$L(f) = \sum_n C(f(x^n), \hat{y}^n)$,其中$n$代表第$n$个数据
\[C(f(x^n), \hat{y}^n = -[\hat{y}^n \ln f(x^n) + (1-\hat{y}^n) \ln (1-f(x^n)) ]\]接下来将$L(f)$对$w$求导,计算可得$w$更新公式为
\(w_i \gets w_i - \eta \sum_n - (\hat{y}^n - f_{w,b}(x^n)) x_i^n\) Logistic Regression与Linear Regression比较如下

在这之后老师介绍了使用Cross Entropy作为目标函数和使用Square Error作为目标函数的不同,介绍了为什么不能在Logistic Regression中用Square Error。
本节介绍的模型称为Generative Model,上一节称为Discriminative Model。他们的不同之处在于Generative对Probability Distribution做了假设 (如假设是Gaussian,或Bernoulli,或Naive Bayes),即Generative包含了人们的先前经验,而Discriminative的performance只受data影响。
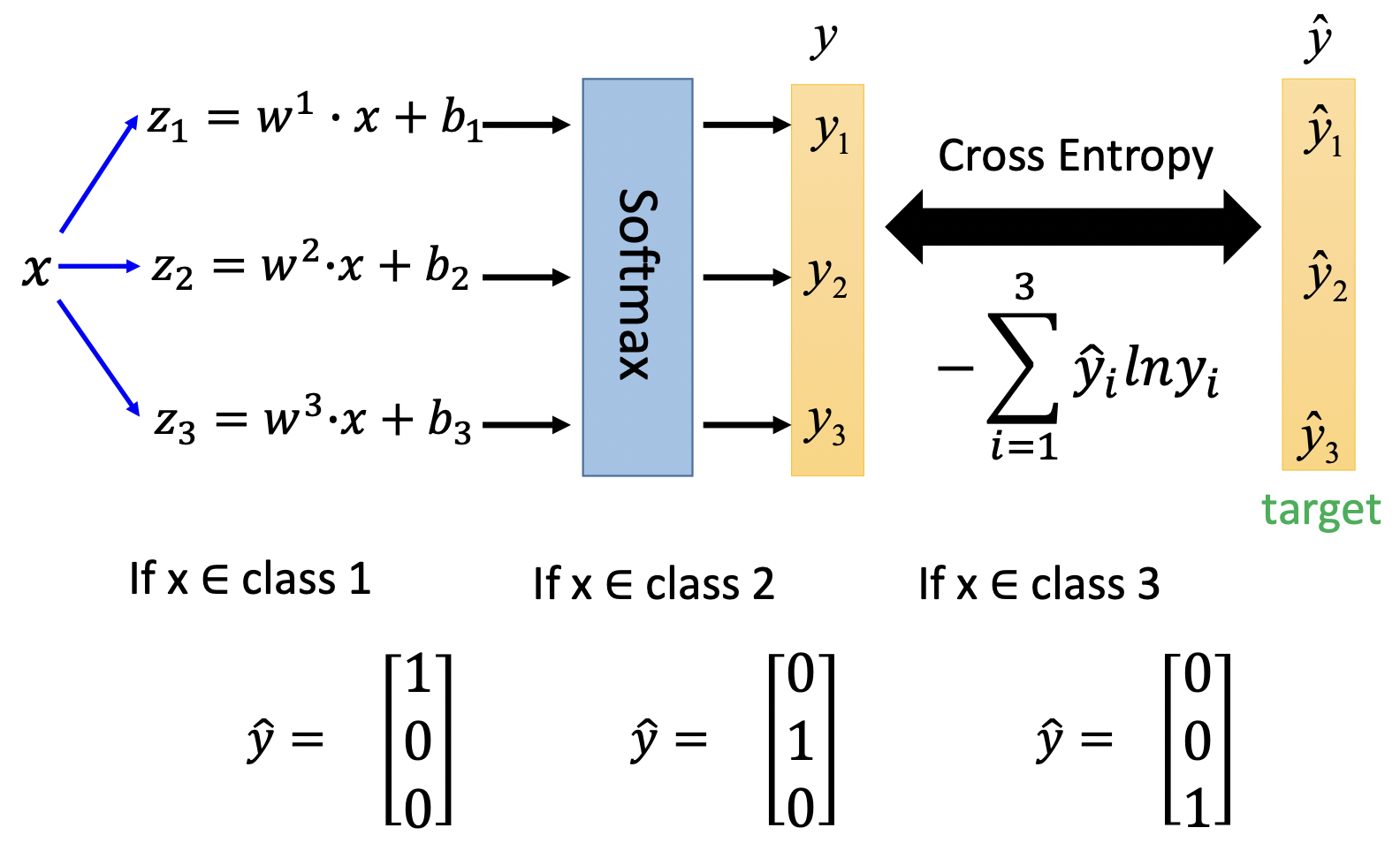
根据二分类可以推广出多分类模型
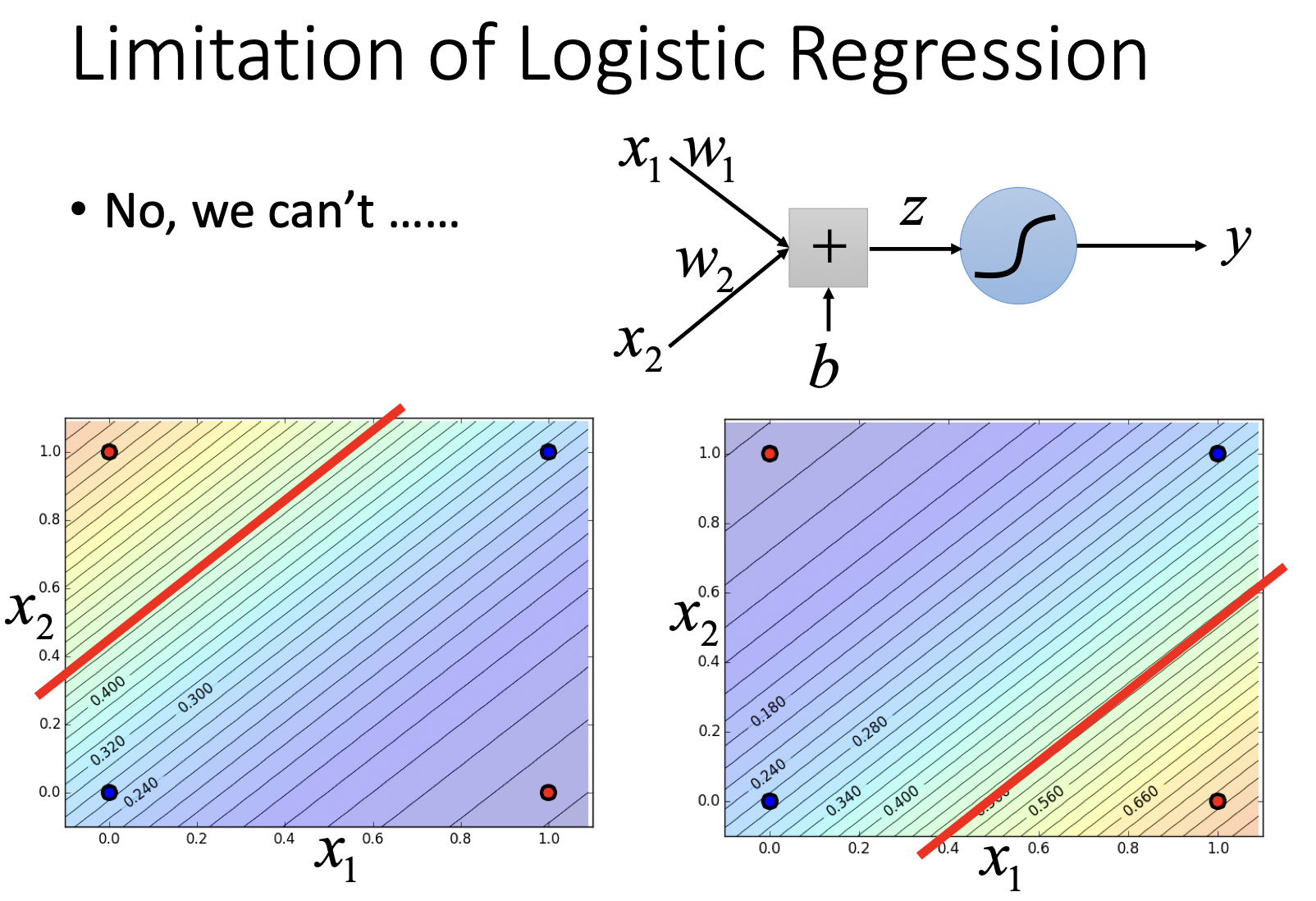
对数据直接进行Logistic Regression局限性很大
我们会增加Hidden Layer,进行feature transform,将原数据映射到新的空间后,在新空间尝试Logistic Regression
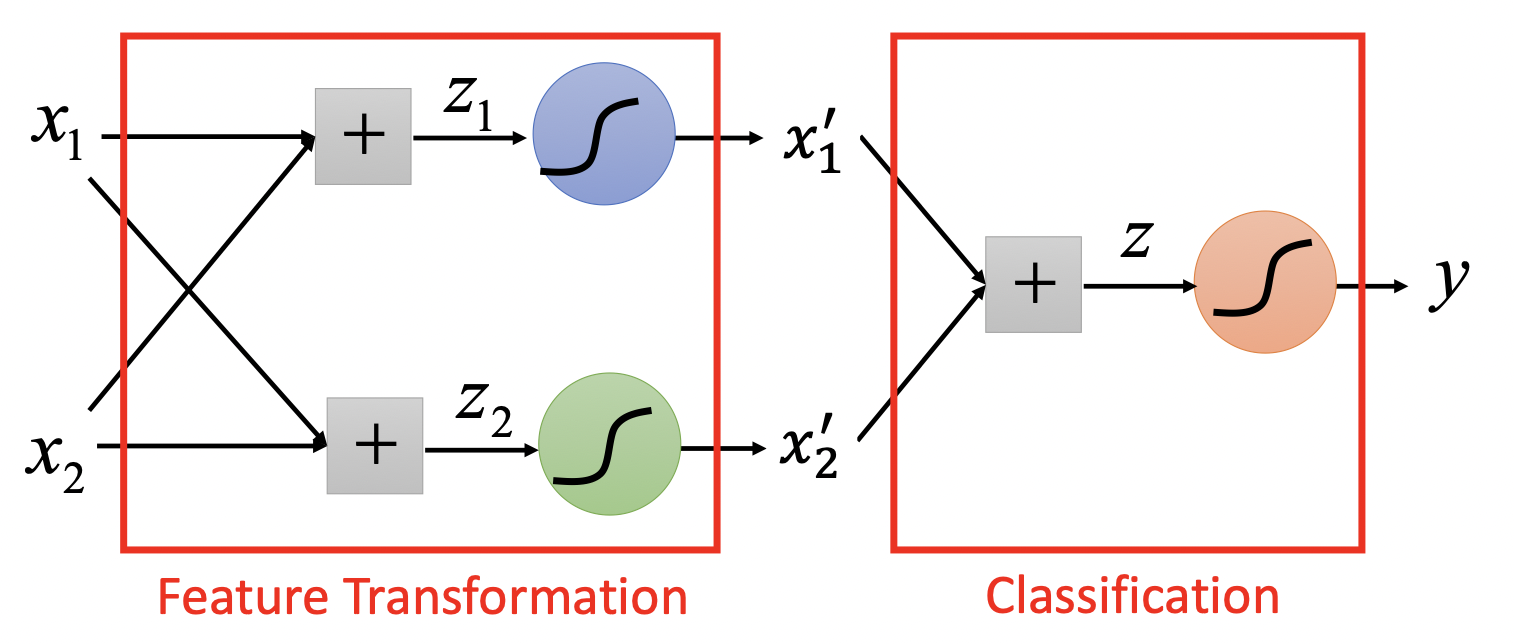
这样就得到了deep learning~
Brief Introduction of Deep Learning
在影音识别领域,ML有较好的表现, 如语音识别,人类无法直接设计出语音的feature,这时候的办法就是丢给ML,让ML自主学习feature;在NLP方面,如情感识别,人类可以设计出一些feature如一些关键性词的存在与否,这时候ML相较于传统方法的进步就不太明显。
“A visual proof that neural nets can compute any function”告诉我们,一个足够“宽”的神经网络 (有足够多的神经元),只需要单层hidden Layer,即可拟合所有$f: R^N \to R^M$,既然如此,Why Deep?
Why Deep?
在构造电路的时候我们可以用两层逻辑门构造一台电脑,但是更建议的做法是使用多层的架构,这更高效而且可以使用更少的逻辑门;Deep Learning大致类似,在不考虑代价的情况下我们可以用一层hidden层拟合函数 (堆非~常多神经元在一层上面),但是更建议的做法是重复利用子模块。
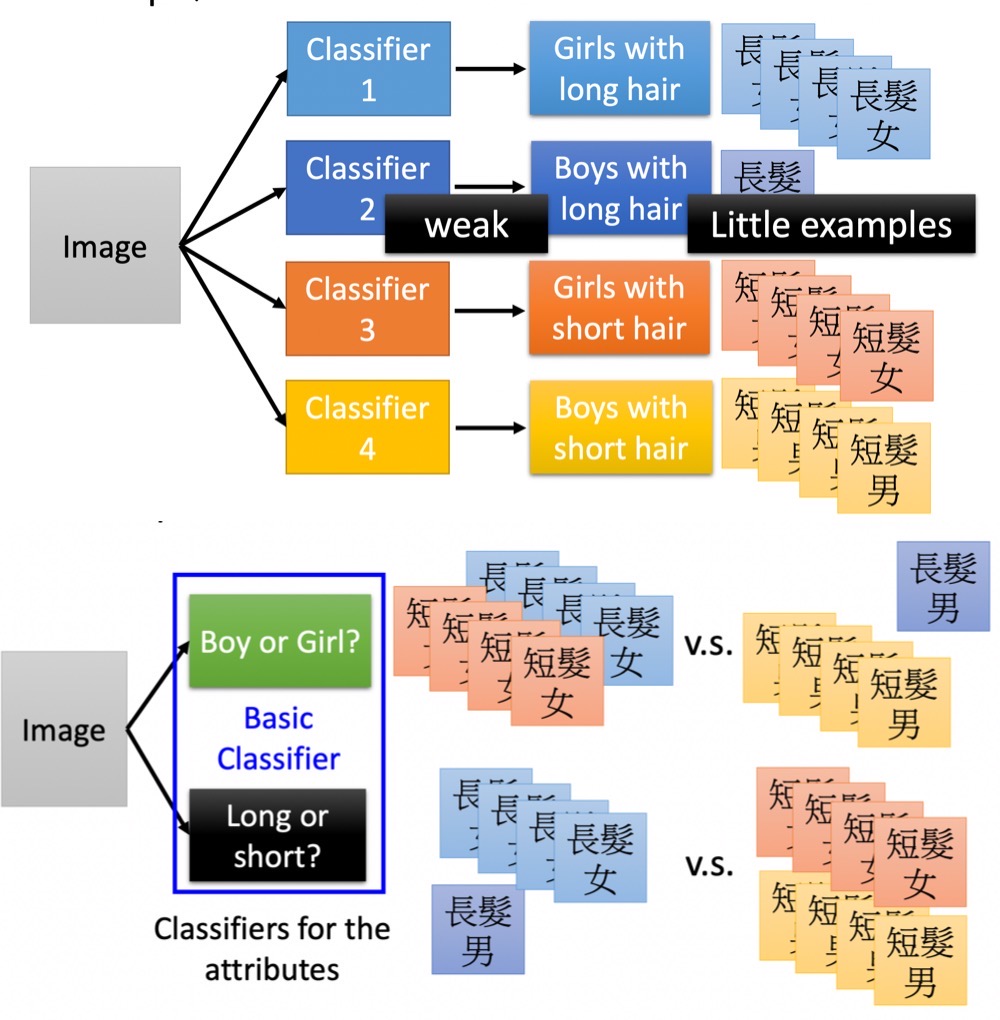
另一方面,子模块的使用缓解了训练中某一类样本过少的问题,如“长发男”样本可能较少,但“长发”,“男”各自的样本较多;如果更高层的classifier利用basic classifier,只需要较少的训练数据,相比之下只用一层classifier嗯训练“长发男”,就比较困难。
在这之后老师用剪窗花的例子解释了hidden layer进行空间对折的作用,介绍了deep在语音识别,图片识别方面与传统方式的比较,最后用手写数字识别的例子形象化的介绍了hidden layer是如何将同类的数据“兜”在一起。

Backpropagation
介绍了链式法则,及在Backpropagation中的应用。
Tips for Training DNN
Batch Normalization
在做Normalization时,我们不是用整个training set计算$\mu, \sigma $,这样做计算量太大,而是对每个batch分别计算$\mu, \sigma$,这种方法叫Batch Normalization。
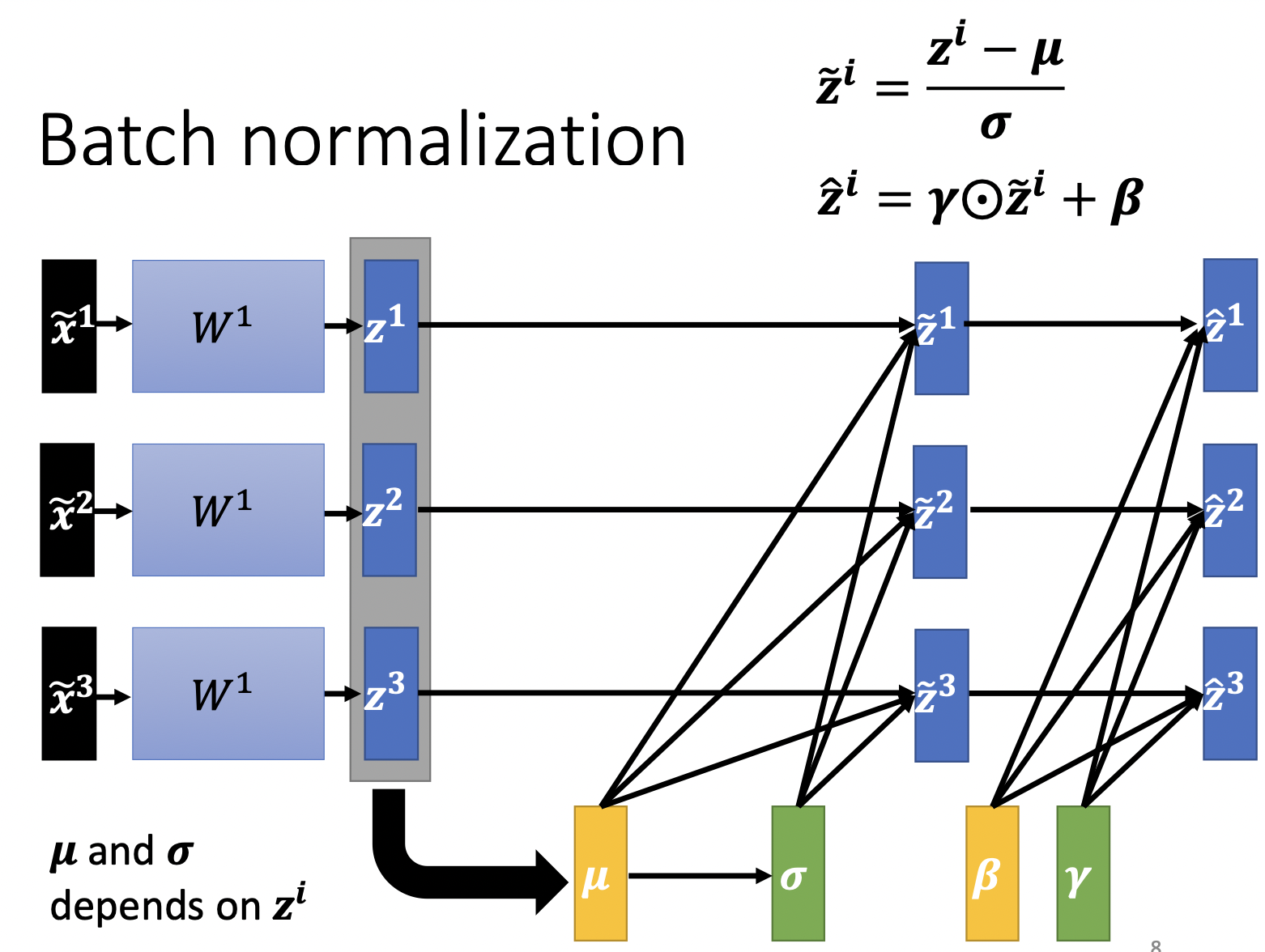
其次,应该不止对输入的$x$做Normalization,$z$也应该做Normalization,因为$z$也可以算作是一次输入。
在Normalization后,可以让$z$再做一次线性变换,$\gamma $初值为全1的vector,$\beta$为全0,让模型自己学习希望的$z$分布。
在test时,并没有batch可以让我计算$\mu, \sigma$,我们可以存下training中的$\mu, \sigma$,根据这些计算test中的数值。
除了Batch Normalization,还有其他 Normalization如Layer Normalization,Instance Normalization等,老师在最后一页PPT给出了参考资料。
Convolutional Neural Network
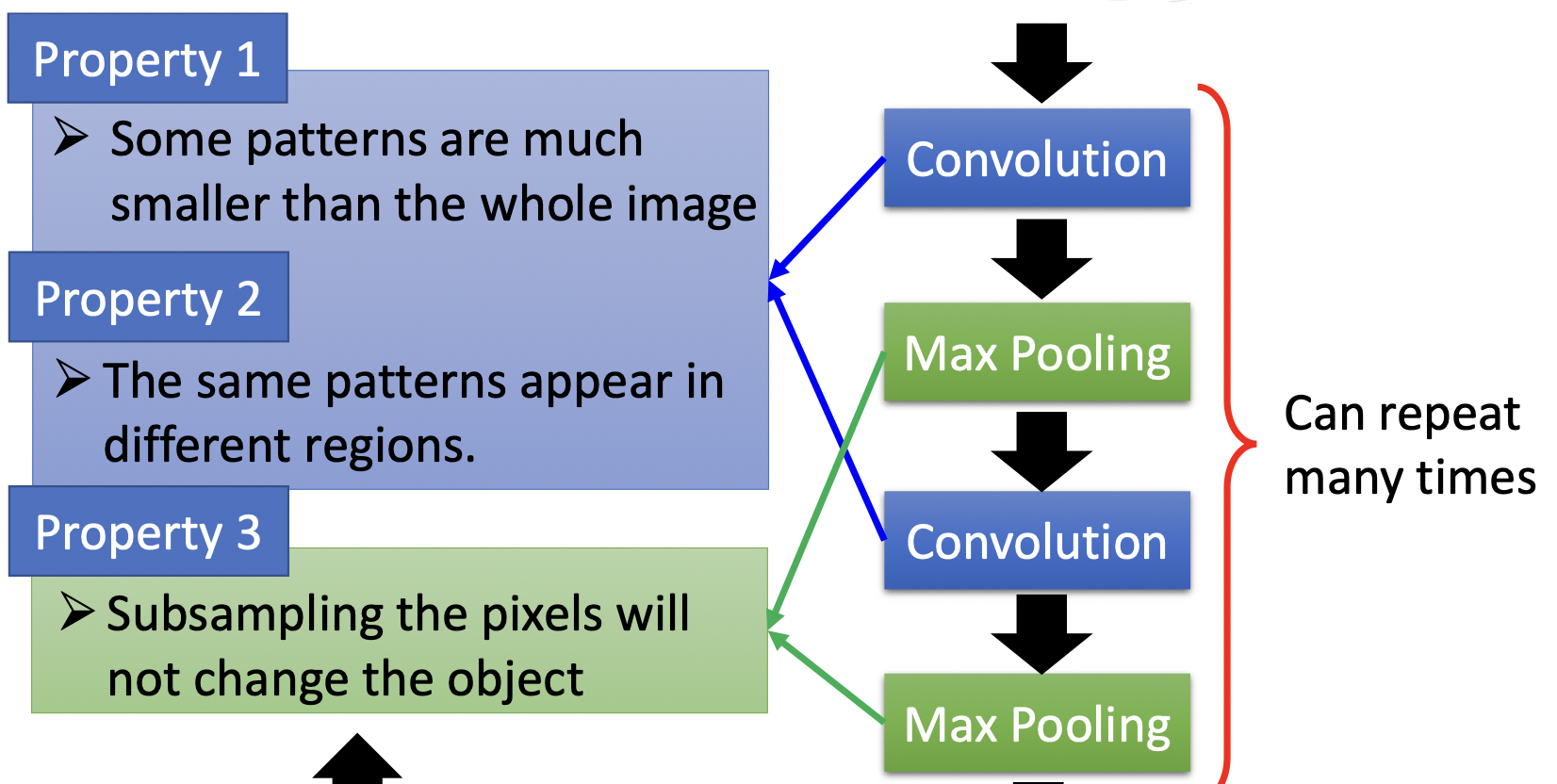
CNN适用于图像处理,是因为存在以下几个观察
- 大部分的pattern比整张image要小,要检测某一个pattern,并不需要neuron连接整个图像。如“鸟嘴”,只需要看到整个鸟图片的鸟嘴部分就可以确定;
- 同样的pattern存在于image的不同区域。在不同的鸟图片中,鸟嘴可能存在于不同位置,有的在左上角有的在右下角什么的,但我们并不需要分别的neuron去检测左上角和右下角,我们用同一个neuron,即他们share同一组参数,减少了参数量;
- image可以做subsampling来减小图片大小,如对一个图片只抽取奇数行和奇数列。
CNN的结构与这些性质相对应
CNN可以检测不同位置的鸟嘴 (平移),但是不容易解决旋转,缩放的问题,DeepMind尝试在CNN前再接一个network,这个network告诉CNN图片的哪些位置需要旋转,缩放,这样会有比较好的结果。
CNN其实是简化的全连接,通过部分连接与共享权值
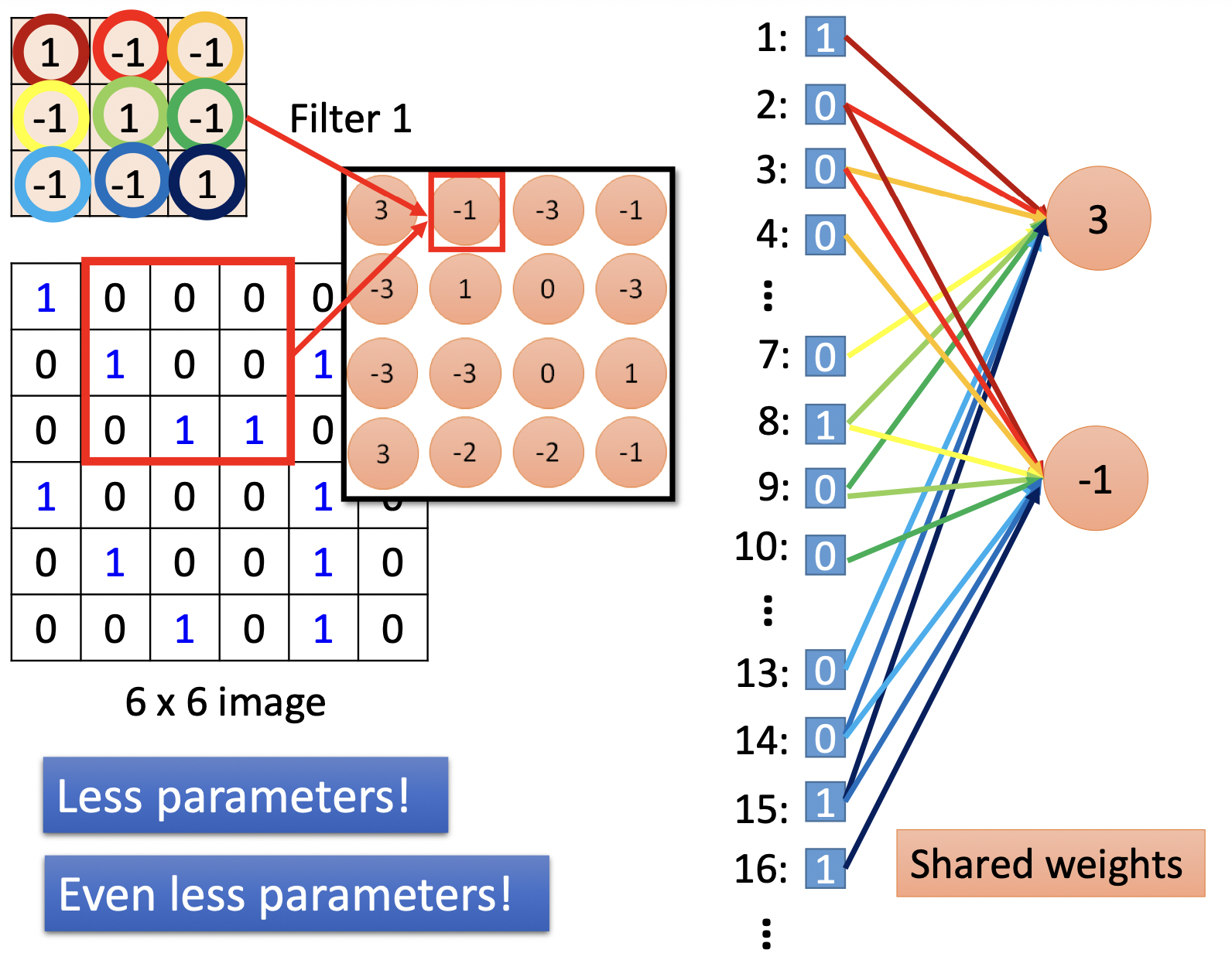
标“3”,“-1”的这些neuron在全连接中将连接所有的pixel,在CNN中他们仅与原图某一小区域的pixel相连,且“3”,“-1”两个neuron共享着权值。
在Convolution层,image通过许多filter,得到不同的feature map,filter的数目就是新image的channel数。
直接考虑高层Hidden Layer在学什么可能比较困难,如第二层hidden layer,一方面他的输入并不是原图像,另一方面,3*3的filter连接的并不是9个pixel (因为前面坐过了Convolution和Max Pooling)。一种方法是训练模型后,固定模型参数,训练模型寻找使某一层hidden layer输出最大的$x$。
使filter (右侧网络模型)各neuron输出最大化的$x$如下,可以看出是每个neuron看起来detect了不同的线条 (图片中显示了重复的纹路)。
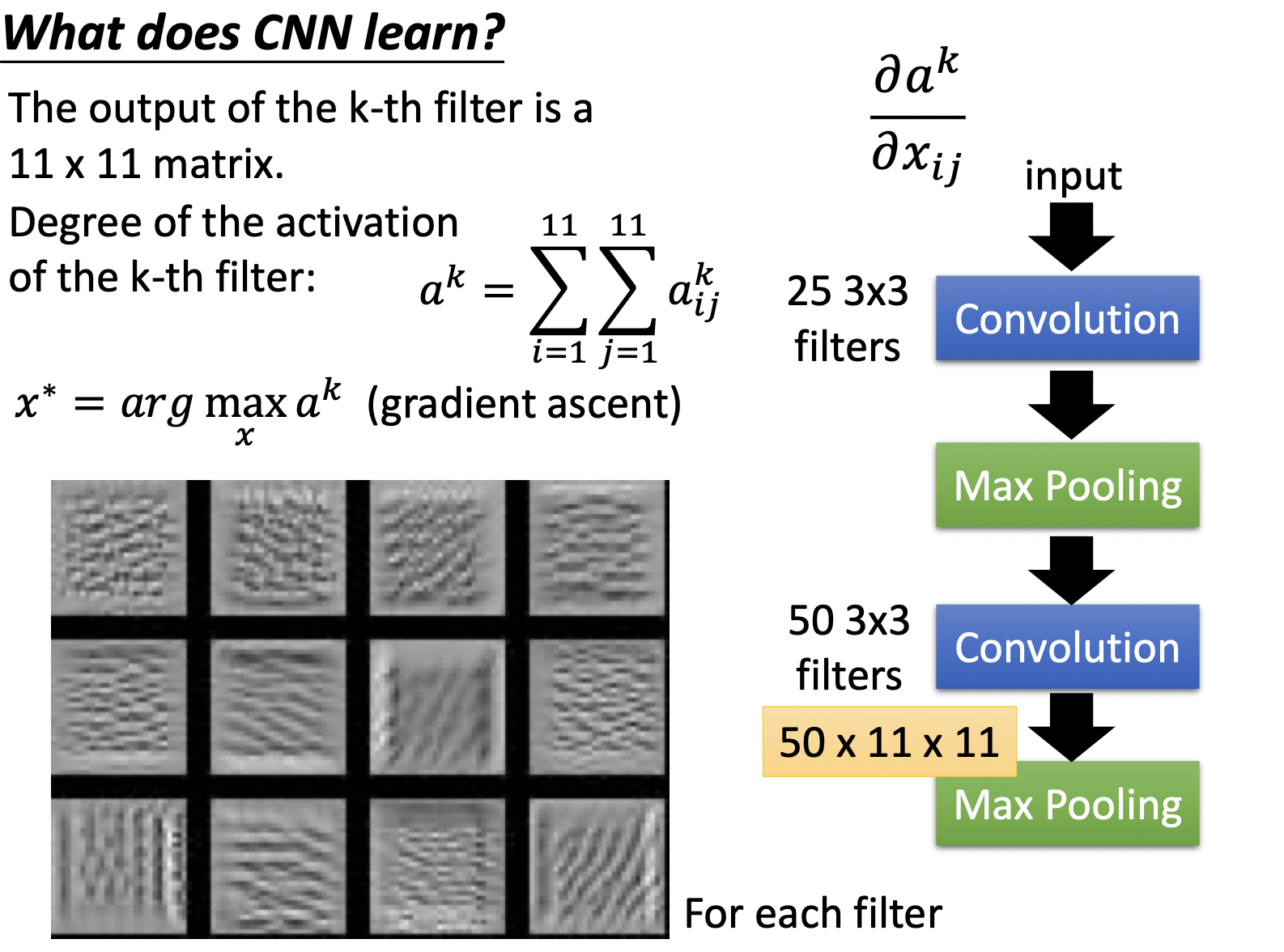
再加上上flatten层 (右侧网络模型),使各neuron输出最大化的$x$如下,加了flatten后,该层看到的是整一个图形,可以看出detect了不同的纹理。
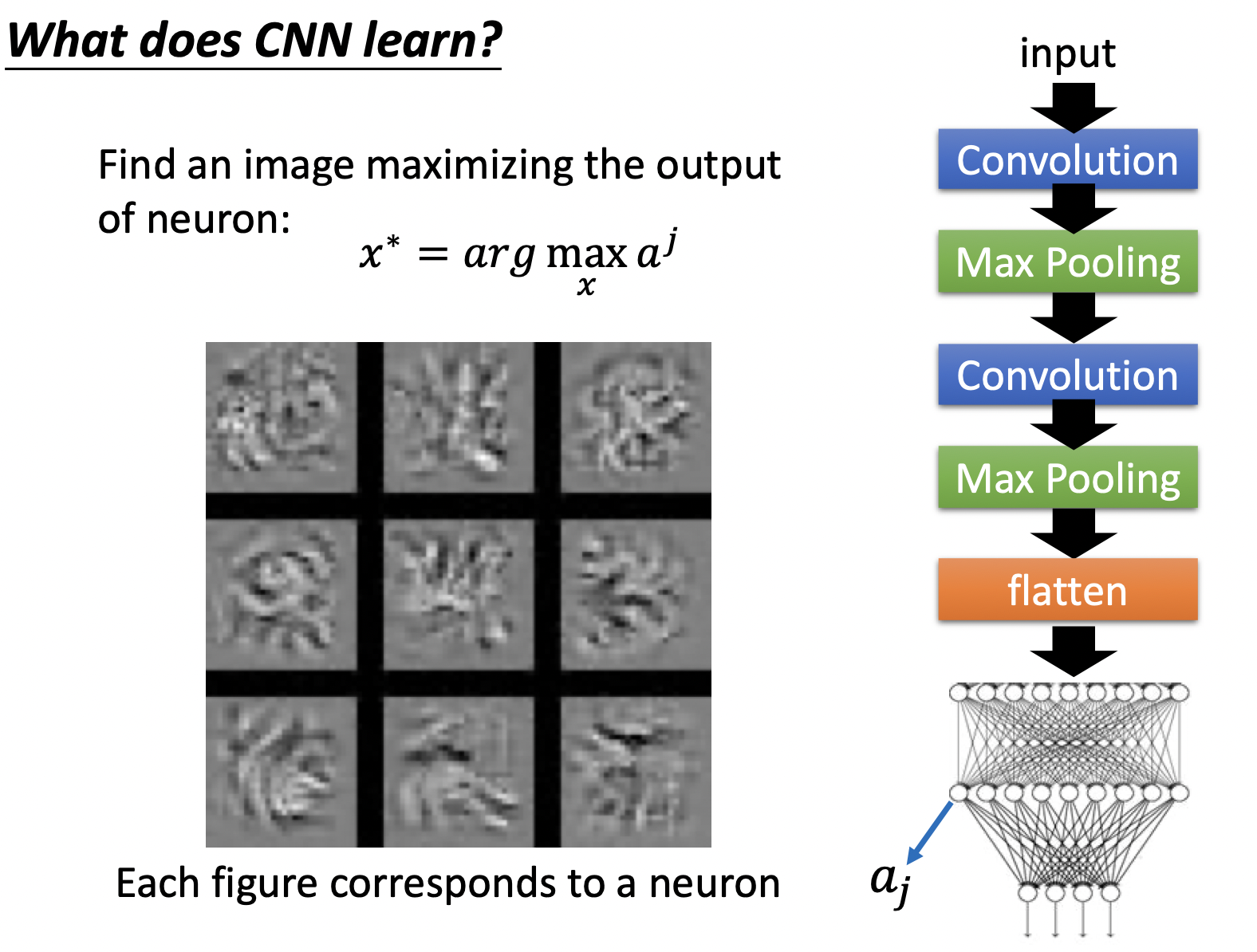
CNN在不同的应用中,应考虑具体的应用的特性,如Alpha Go使用了CNN的模型,但围棋并不存在可以subsampling的性质,所以Alpha Go并没有采用max pooling;在语音识别中,CNN卷积中filter只考虑Frequency方向的移动等。
Self-Attention
Chinese 1 Chinese 2 English 1English 2 ppt pdf
Self-Attention与CNN存在一定的关联性,可以认为CNN人为规定了filter,且receptive field范围较小,Self-Attention关注整个vector set,他自主学习filter的大小及值,而这些在CNN中是人为规定的。
在https://arxiv.org/abs/1911.03584中用数学的方式证明了CNN是Self-Attention的一个特例,Self-Attention的function set包括这CNN的function set。
2021年的课程并不包括RNN了,RNN的角色很大一部分可以被Self-Attention取代,Self-Attention主要的问题在于运算量非常的大,减少其运算量是未来的重点,在Efficient Transformers: A Surve中介绍了各式各样的transformer的变形。
Transformer
Chinese 1 Chinese 2 English 1English 2 ppt pdf
seqseq用于解决QA的问题,即输入一个序列输出一个序列。
原始的Transformer架构也许并不是最optimal的,研究人员也做了其他的尝试,如On Layer Normalization in the Transformer Architecture中改变了Layer Norm的位置,PowerNorm: Rethinking Batch Normalization in Transformers,比较了不同的Normalization的表现。
原论文中decoder及encoder都可以有多层,encoder在Cross Attention时均采用了最后一层decoder的输出,也可以采取其他的新的方法。
Pointer Network拥有从输入复制东西到输出的能力。
如果对模型学到的attention的基本架构有一定要求,可以看看Guided Attention。
Beam Search
假设有一个字典为${ A, B }$的输出任务。Transformer的decoder,在第一步选中概率最大的$A$作为第一个输出,根据第一个输出继续产生第二个输出$B$…最终得到输出序列$A, B , B $,即图中的红色箭头路径,。这是Greedy Search。·
但有可能存在绿色路径这样的路径,虽然在第一个位置该路径的概率小于红色路径,但总表现优于红色路径($0.6 * 0.6 * 0.6 < 0.4 * 0.9 * 0.9$)。暴力遍历搜索树上所有路径显然是不可行的,Beam Search用于test过程,尝试寻找全局最优路径。
在翻译任务,语音识别任务中,最优的输出是确定的,Beam Search适用于该类任务,但对于需要机器发挥自己的“想象力”的任务,如给定上文输出下文,Beam Search容易重复输出机器找到的“最优”的那个,而不容易有好的结果。这是一件很神奇的事情,在其他模型训练时会人为引入一些Noise,为了使机器在test中有更好的表现;而在decoder部分是在test时引入noise,因为我们有时希望decoder表现出一些随机性。
BLEU score?
在使用监督学习训练transformer时,对于每一个输出元素,minimize的是cross entropy,而在最终评估时,用的却是Blue score (比较的是两个序列),minimize cross entropy,不一定可以maximize blue score。由于blue score是不能够微分的,一种方法是使用RL (不知道怎么optimize的时候就用RL就好了!)
exposure bias
在训练的时候,输入encoder的是正确的序列,但是在test的时候,显然无法获得正确的序列。encoder如在某一步输出了错误的答案,很容易出现一步错步步错的现象,一种方法是Scheduled Sampling。
Generative Model
机器学习处理的问题可分为监督学习任务与无监督学习任务两种。我们以上介绍的均为supervised learning ,包括classification任务和regression任务;另一种是unsupervised learning,包括聚类任务以及Generative modeling,无监督学习的算法包括K-means及Generative Adversarial Networks等。我们将介绍生成模型Generative modeling,以及生成对抗网络GAN。
Discriminative vs. Generative Modeling
在监督学习中,我们尝试开发模型来预测一个输入的类标签,这种预测性的建模任务被称为分类classification,也被称为Discriminative Model。
显式或隐式地对数据分布进行建模的方法被称为Generative Model,通过对拟合的数据分布进行抽样,可以在输入空间生成新的数据点。例如,我们目前的数据可能符合高斯分布,Generative Model总结这种数据分布,并生成符合已知数据分布的新数据。
设希望拟合的数据分布为$y_{data}$,Generator拟合的结果是$y_G$,输入中的$z$是从某种简单的数据分布抽样的,作为生成过程的种子。经过Generator,输入将对应到分布$y_G$中的某个抽样,即模型生成了新的数据。
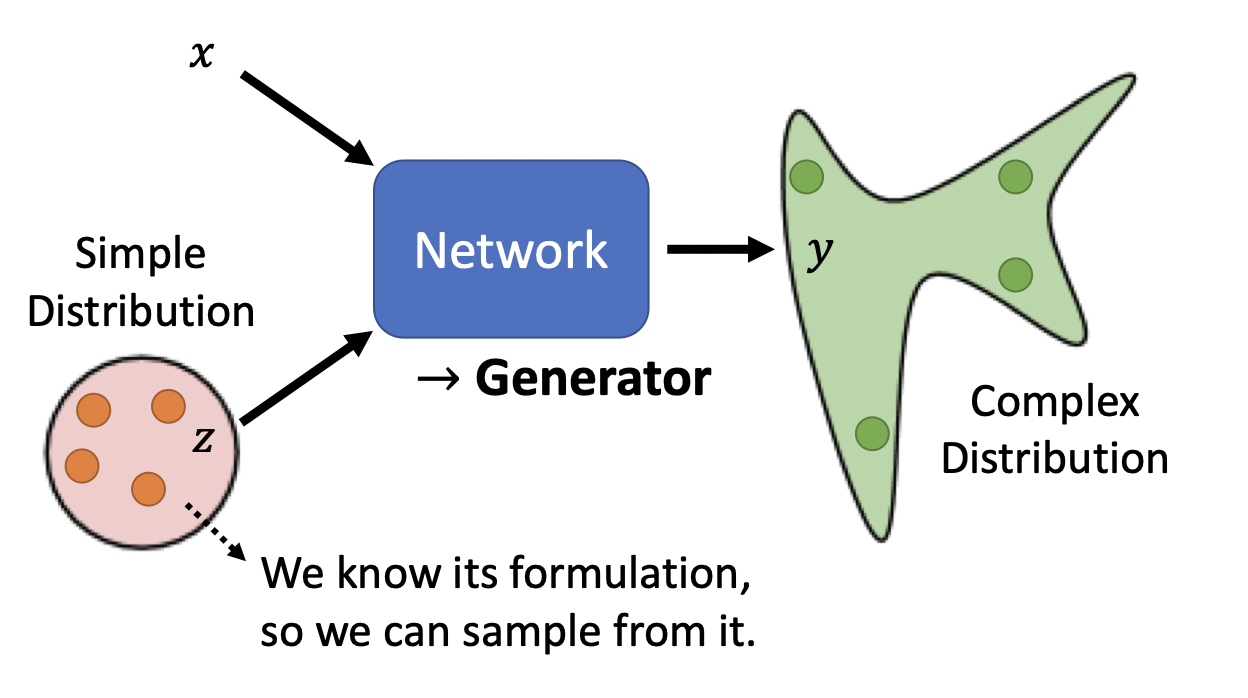
A Gentle Introduction to Generative Adversarial Networks (GANs) by Jason Brownlee on June 17, 2019
The generator model takes a fixed-length random vector as input and generates a sample in the domain.
The vector is drawn from randomly from a Gaussian distribution, and the vector is used to seed the generative process. After training, points in this multidimensional vector space will correspond to points in the problem domain, forming a compressed representation of the data distribution.
This vector space is referred to as a latent space, or a vector space comprised of latent variables. Latent variables, or hidden variables, are those variables that are important for a domain but are not directly observable.
我是这样理解的。。如图片,同一类图片在高维空间内也许符合某种分布,只要我们学到了该分布,便可以生成新的图片。
GAN
Theory of GAN and WGAN: Chinese English
Evaluation of GAN and Conditional GAN: Chinese English
GAN: Generative Adversarial Nets
GAN包括一个Generator以及一个Discriminator,他们互相对抗、进化。如生成人脸图像任务,假设目前有一个人脸图像数据库,Generator接受一个noise输入 (从一个简单分布随机抽样来的),输出一个人脸图像,Discriminator是一个分类器,他从数据库中sample出一部分人脸图像,并尝试分辨Generator生成的图像与数据库中的图像的区别。
更形式化的描述是:
现有数据库数据为$x$,数据分布为$p_{data}$;
Generator的输入为,某简单分布 (如高斯分布,正态分布等)的随机抽样$p_z(z)$,Generator将数据空间映射到$G(z;\theta_g)$,其中$G$为可微分函数,其函数参数为$\theta_g$,学习到的分布称为$p_g$,$p_g$是对$p_{data}$进行拟合的结果;
接下来是Discriminator,他表示为$D(x; \theta_d)$,他的输出为一个标量,表示$x$来自$p_{data}$的概率;
我们训练D,让他尽可能的区分开训练数据及$G$生成的数据,及使样本分配正确标签的概率最大化,即$D^* = \arg \max _D V(D,G)$,$V(D,G)$为$D$的objective function,在最早提出他的论文中,$V(D,G)$如下
\[V(D,G) = E_{x \sim p_{data}}[log D(x)] + E_{z \sim p_z(z)}[log(1-D(G(z)))]\]其中,$E_{x \sim p_{data}}[log D(x)]$代表抽样自$p_{data}$且正确分类的期望,$E_{z \sim p_z(z)}[log(1-D(G(z)))]$代表抽样自$p_g$且正确分类的期望,写成这样是为了将$D$,当作一个Classifier,$V(D,G)$形式上就像cross entropy,后来研究人员发现此形式下的$max_D V(D,G)$与$p_g, p_{data}$的JS距离有关;
我们也训练$G$,让$p_g$和$p_{data}$越接近越好,即 \(G^* = \arg \min _G Div(p_g, p_{data})\) ,不知道怎么算$Div$?没关系,训练$D$,看他的$V(D,G)$可以有多大,该最大值就与$Div$有关。直观来想,$D$分类正确率却高,说明$p_g, p_{data}$差距越大,即他们的$Div$越大。最后得到$G^* = \arg \min_G \max_D V(D,G) $。
除了JS div,在https://arxiv.org/abs/1606.00709中详细介绍了其他div以及如何设计objective function。
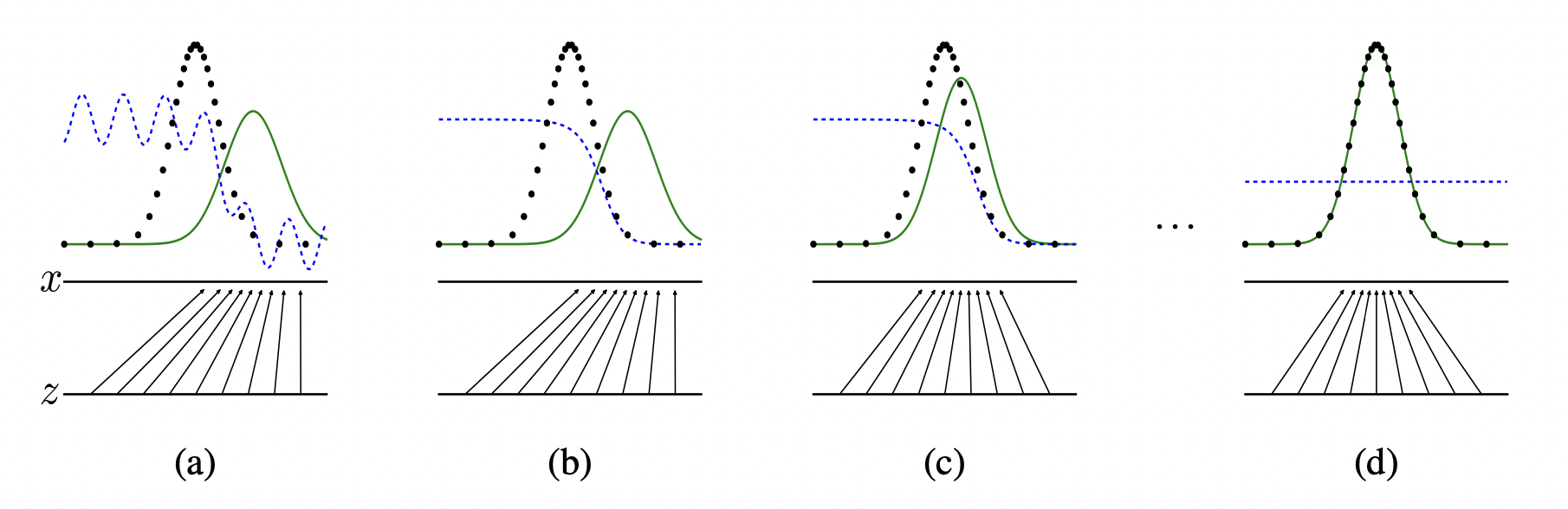
上图中,蓝色线代表$D$分布,黑色线代表$p_{data}$,绿色线代表$p_g(G)$,$z$表示抽样出的噪声,输入$G$,$x = G(z)$代表$G$的输出,两个水平线之间的箭头展示了$G$是如何进行数据空间映射的。
(a),进行$D$,$G$的初始化;
(b),训练$D$分辨来自$p_g, p_{data}$的数据,discriminative distribution (蓝色线) 改变;
(c),训练$G$,根据D的梯度,使$G(z)$流向更容易被分类为数据库数据的区域;
(d),经过多次训练后,如果达到$p_g = p_{data}$,$G,D$两者将都不能改进,$D$无法区分这两个分布, $D(x) = 1 / 2$。
算法流程

WAN
在GAN中使用JS距离有一个问题,在大多数情况下$p_g$与$p_{data}$是不重叠的,就算有重叠,经过sampling也很难重叠。如果两个分布不重叠,二元分类器就能达到100%的准确率。那么在GAN训练期间,准确率(或损失)毫无意义,如下图,虽然中间的比左边的比已经有接近了,但是JS距离依然是$log2$。
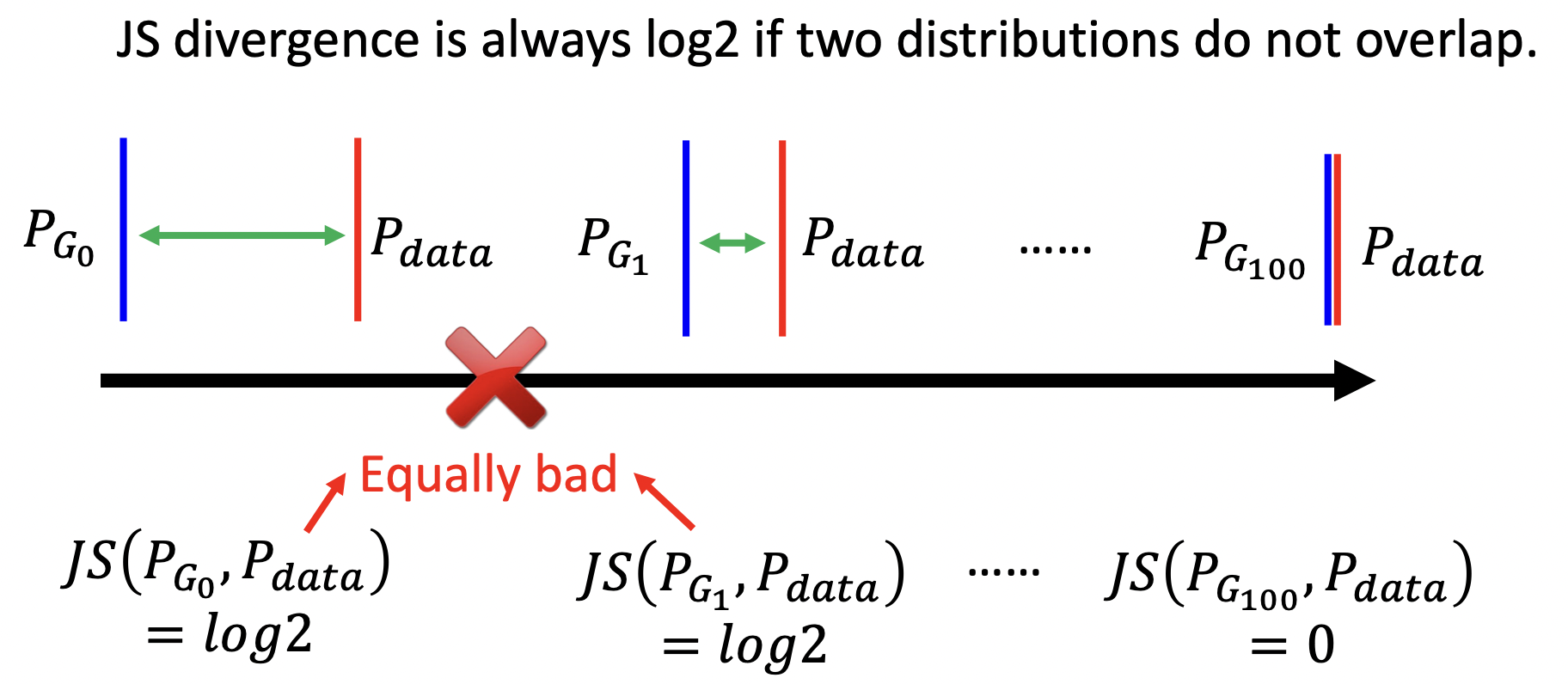
Wasserstein distance是另一种$Div$度量方式,假设有$P_1, P_2$两种概率分布,Wasserstein distance直观上可以理解为在最优路径规划下,把土堆P1挪到土堆P2所需要的最小消耗,所以Wasserstein距离又叫Earth-Mover距离。
Wessertein距离相比KL散度和JS散度的优势在于:即使两个分布的支撑集没有重叠或者重叠非常少,仍然能反映两个分布的远近。而JS散度在此情况下是常量,KL散度可能无意义。
\[W(p_{data}, p_g) = \max_{D \in 1 - \text{Lipschitz} } \{ E_{x \sim p_{data}}[D(x)] - E_{y \sim p_g}[D(y)] \}\]其中$D \in 1 - \text{Lipschitz}$要求$D$尽可能平滑。
GAN依然是一个非常难train的问题,关于GAN李宏毅教授有更详细的课程在这里。
CycleGAN
Self-supervised Learning
- Youtube:
- Slides:
- HW7: BERT
- HW8: Anomaly Detection
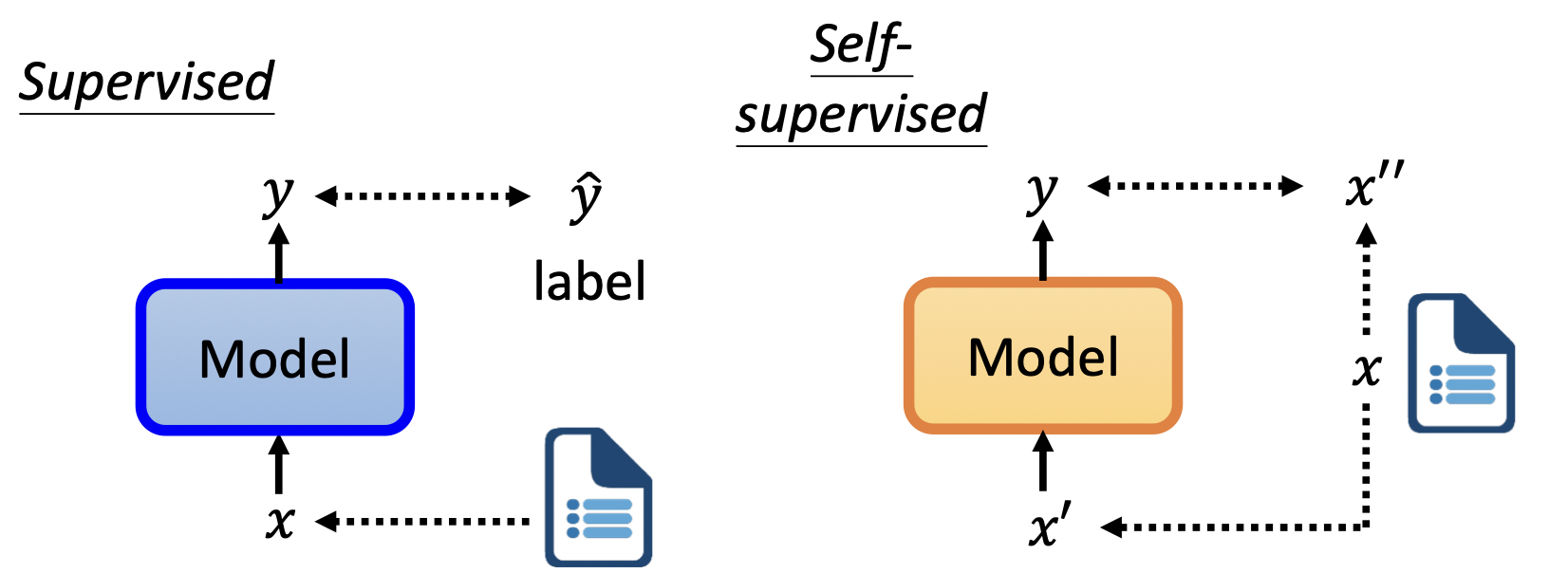
Self-supervised Learning可以看作是unsupervise learning的一种,系统尝试用输入的一部分预测另一部分。
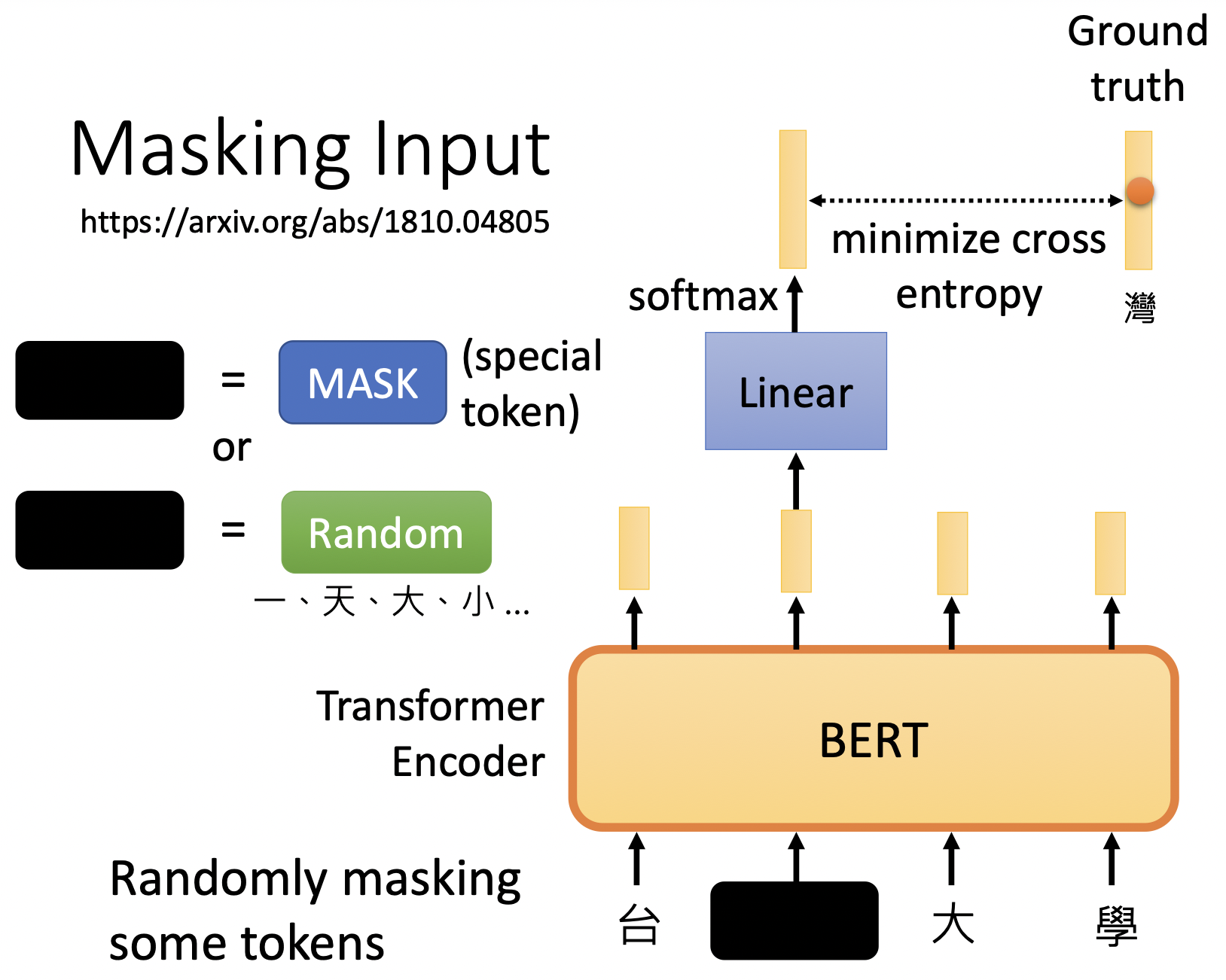
要实现Self-supervised Learning,BERT中使用了以下方法。
maks input:随机盖住一些token,并预测这些盖住的token,盖住的token可以用一个代表mask的特殊token代替,也可以使用一个random的token代替;input经过BERT得到token的embedding,接着经过linear以及分类器得到预测值;mask会执行多轮,每次随机盖住部分input执行预测;其中token是自定义的序列的组成单位。
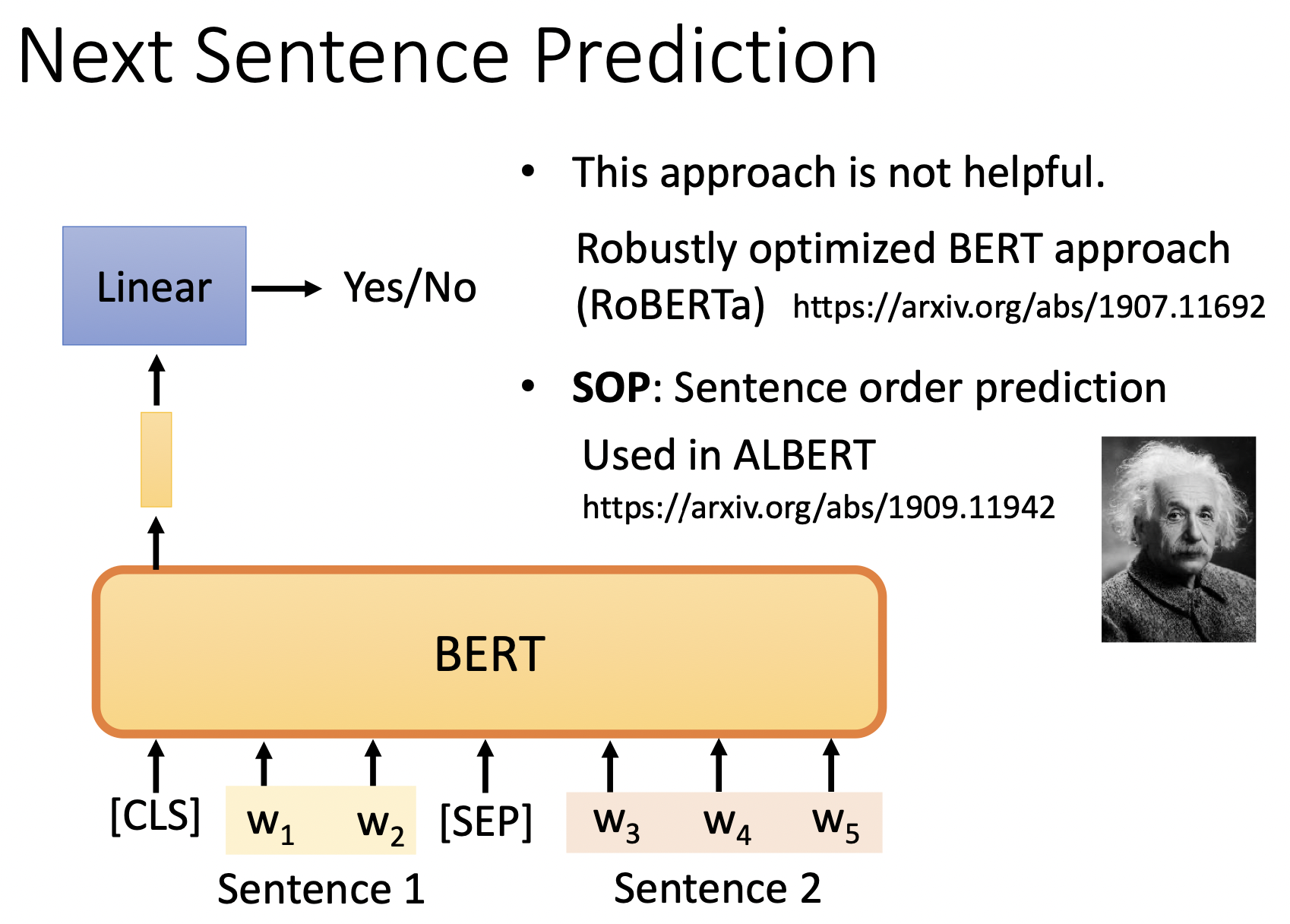
next sentence prediction :输入两个句子,预测它们是否有先后关系。
使用无标注数据训练BERT后 (该步骤称为Pre-train),对应不同的下游任务,我们会使用少量标注数据微调 (Fine-tune )。
BERT内部结构为transformer的encoder部分,一个token的含义与他的上下文息息相关,当想要预测mask的部分时候,BERT就借助了该token的上下文信息。
与BERT不同,GPT为transformer的decoder部分 (除了transformer中encdoer向decoder传递信息的那个self-attention),使用预测下一个token的方式进行pre-train;GPT可以做Generation任务。
Adversarial Attack
Adversarial Attack: Basic Concepts: Chinese English
Adversarial Attack: Attack and Defense: Chinese English
要将类神经网络真正应用到实际中,除了要求模型拥有较高的正确率,还需要能应对来自人类的恶意,就算人为的欺骗network,network也应该拥有高正确率。
How to Attack
神经网络看到的世界与人类认知里是不同的,如之前的手写数字识别 (CNN)中提到的,通过固定模型参数,调整输入数据,得到最大化CNN的输出的图像是下面这样子的,(即神经网络“认为”最像$0,1,2,\dots$的图片),在人看来,这就是一些不知所云的噪点嘛!

同样的,在图片中加入一些noise后,也许人无法肉眼分辨出差别,但对于神经网络而言,他看到的图片却发生了天差地别的变化,

左边的猫是原始图像,我们50层的ResNet认为有64%的可能,这是一只虎皮猫,右边的猫是加入了noise后的图像,ResNet就100%确定他是一只海星了,下图是将两个图片做差并将差距放大50倍的图像。

设原数据为$x^0$,对应的label为$f(x) = y^0$, 攻击过程就是寻找一个与$x^0$非常相近的$x$,而$f(x)$与正确的$\hat{y}$相差甚远。在训练过程中,network的参数固定,使用梯度下降法调整$x$。
攻击可分为Non-targeted与Targeted两种,其中Non-targeted无目标攻击表示我们 (攻击者)并不指定$f(x)$是什么,只要识别结果不正确就好了了,其loss函数定义如下,其中$e$代表交叉墒,代表$y$与$\hat{y}$的距离;
而Targeted表示我们不止希望$f(x)$与正确的$\hat{y}$相差甚远,更希望$f(x)$接近$y^{target}$。
\[L(x) = -e(y, \hat{y}) + e(y, y^{target})\]最终得到的$x$除了loss尽量小,还需要与原$x^0$ 的差距尽量小
\[x^* = \arg \min_{d(x^0, x) \le \varepsilon } L(x)\]其中$d(x^0, x)$当然有多种评价标准啦,需要考虑不同领域人类的感知能力。如在图片识别中,人类对每一个pixel的微小改变的感知能力就不如单pixel的大变化。
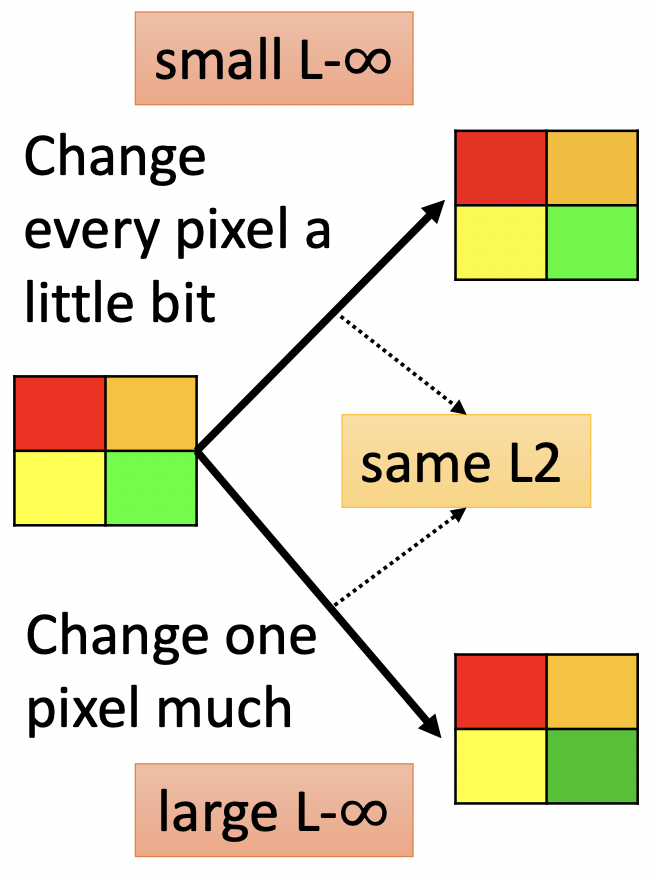
这种情况下L-$\infty$比L2更合适,因为L-$\infty$检测的是$x$多维度上的最大变化:
\[\begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \dots \end{bmatrix} - \begin{bmatrix} x_1^0 \\ x_2^0 \\ x_3^0 \\ \dots \end{bmatrix} = \begin{bmatrix} \Delta x_1 \\ \Delta x_2 \\ \Delta x_3 \\ \dots \end{bmatrix} \\ d(x^0, x) = \| \Delta x \|_ \infty = \max \{ \mid \Delta x_1 \mid, \mid \Delta x_2 \mid,\dots \}\]在Gradient Descent的过程中,为了达到上述约束,在每次update之后判断一下$d(x, x^0)$,如果不符合约束,就对$x$作出调整。
${\color[RGB]{159,46,39}{\text{Algorithm: Gradient Descent}}}$
原图像为$\mathbf{x}^0$,$\mathbf{x}^t$为attacked image,初始化为$x^0$
\[\begin{align} & \ \ \text{for }t=1 \text{ to }T:\notag \\ & \ \ \ \ \ \ \mathbf{x}^t \gets \mathbf{x}^{t-1} - \eta \mathbf{g} \notag \\ & \ \ \ \ \ \ \text{If } d(\mathbf{x}^0, \mathbf{x}) > \varepsilon \notag \\ & \ \ \ \ \ \ \ \ \mathbf{x}^t \gets fix(\mathbf{x}^t) \notag \end{align}\]其中,
\[\mathbf{g} = \begin{bmatrix} \frac{\partial L}{\partial x_1} \mid _{x = x^{t-1}} \\ \frac{\partial L}{\partial x_2} \mid_{x = x^{t-1}} \\ \frac{\partial L}{\partial x_3} \mid_{x = x^{t-1}} \\ \dots \end{bmatrix}\]
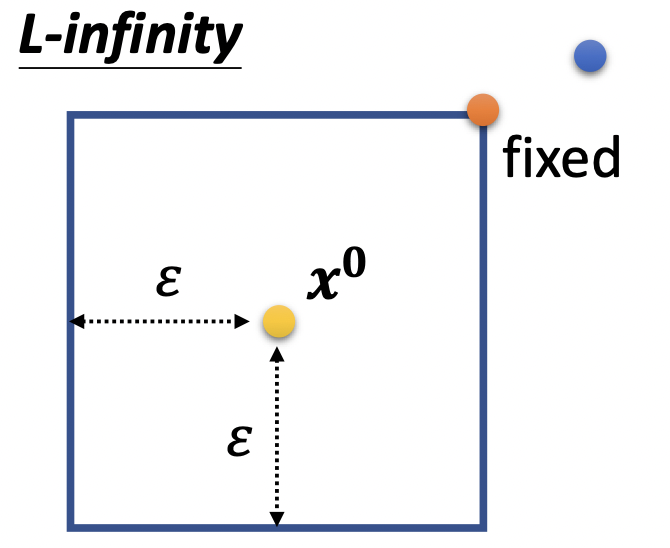
如果使用的$d(x^0, x)$为L-$\infty$,图示如下,黄色点为原图像$x^0$,黑色框框为修改后的$x$可存在的范围,蓝色点为update后的$x$,update后发现超出框框了,修正到橘色点,修正的方法可以有很多种,如在框内寻找距离蓝色点最近的一个点作为修正后的结果。
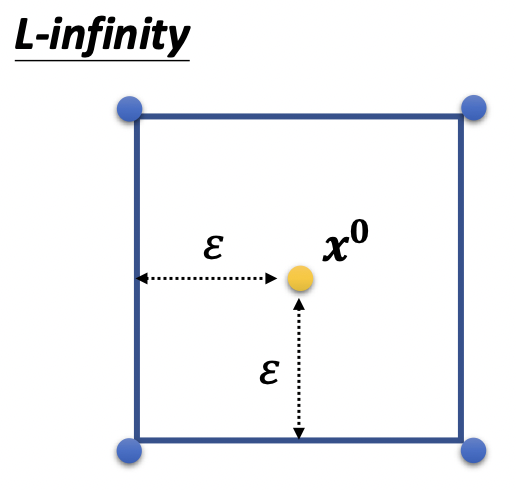
Fast Gradient Sign Method (FGSM)提出仅仅对原$x^0$作出一步修改 ($T = 1$),尝试达到很好的效果。
算法大致过程如下
${\color[RGB]{159,46,39}{\text{Algorithm: Fast Gradient Sign Method}}}$
原图像为$\mathbf{x}^0$,$\mathbf{x}^t$为attacked image,初始化为$x^0$
\[\mathbf{x}^t \gets \mathbf{x}^{t-1} - {\color{Orange}{ \varepsilon } } \mathbf{g} \notag\]其中,
\[\\ \mathbf{g} = \begin{bmatrix} sign \Big( \frac{\partial L}{\partial x_1} \mid _{x = x^{t-1}} \Big) \\ sign \Big( \frac{\partial L}{\partial x_2} \mid _{x = x^{t-1}} \Big) \\ sign \Big( \frac{\partial L}{\partial x_3} \mid _{x = x^{t-1}} \Big) \\ \dots \end{bmatrix} \\ sign(t) = \begin{cases} 1 & \text{ if } t > 0 \\ -1 & \text{ otherwise } \end{cases}\]
即update过后,蓝色的点降落在框框的边缘,具体细节在原论文。
Black Box Attack
上面说的方法都是白箱攻击啦,因为我们在进行梯度下降的时候需要知道要攻击的模型的参数,与之相对的就是黑箱攻击。
在不知道目标网络参数的情况下,如果我们知道目标网络训练数据,那么可以尝试用这些训练数据训练另外一个proxy网络,那么如果可以攻击这个proxy网络,也许就能攻击目标网络。就算不知道训练模型,我们也可以通过向线上的模型丢一些输入进去,得到输出。黑箱攻击虽然比白箱攻击困难一点,但是也不是不可能成功的。想要攻击成功,比我们想象中简单,如识别是一只猫的图片,高维空间中只有很小一部分范围内可以将该图片识别为猫,一些微小的扰动就会让图片掉出该范围。
除此之外, 还有One pixel attack,即尝试只修改图片中一个pixel达到attack的效果,Universal Adversarial Attack,尝试用一个通用的噪点在多种图片 (猫,狗,火炉…)上达到attack效果….,尝试在真实世界中攻击 (与单张图片,对物品将会多角度、多距离观察) 等等等等。
Defense
防御方法可以分为:主动防御Passive Defense,被动防御Proactive Defense两种。主动防御指在test过程中,图片输入模型前进行一些处理,如模糊化,压缩等,尝试去除输入图片中可能的人为noise带来的影响;被动防御指在train过程中,对原训练数据,用可能的attack方法添加噪声,将attacked image的标签设置为正确标签进行训练,这种方法扩大了数据集,某种程度上是一种Data Augmentation的方法。
Explainable AI
上面我们也提到过,机器学习看到的世界与人类看到的并不相同,CNN坚信是数字的图片,在人类看起来就是一堆噪点;神经网络像个黑盒子,我们投进去一些输入,得到输出,效果不好就暴调一下超参数…效果好了就结束,不知道中间发生了什么;另一方面,一些强有力的神经网络拥有较差的解释性,这并不是我们拒绝它们的原因,linear model拥有高可解释性,我们可以知道每个feature对应的weight是多少,我们知道每个feature起了多大的作用,但同时linear model在复杂任务上的表现差强人意。
Explainable AI尝试对AI做出解释,如果可以知道AI是如何做出判断,为何做出这样的判断的话,对我们的训练可以有帮助,也会让我们的老板开心。Explainable ML包括Local Explanation,Global Explanation,局部解释指,对特定的图片,询问AI为什么做出这样的决定 (为什么AI认为这张照片是猫咪);全局解释不对应特定的图片,而是询问AI什么样的输入可以得到对应的输出 (AI心目中的猫咪是什么样子的)。
Local Explanation
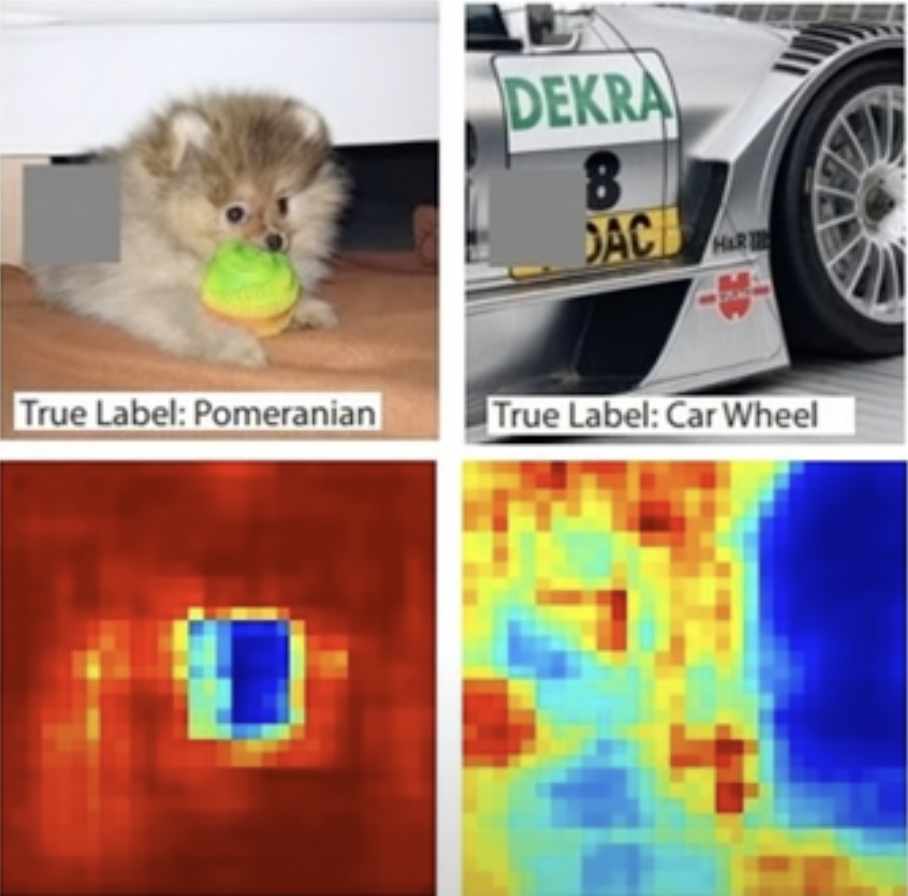
对于输出的图片,我们可以对其中的小部分进行遮盖,查看神经网络做出的决策有多大的变化,决策变化越大, 说明盖住的那部分越重要。
下图中越偏蓝色的部分,表示决策变化越大,可以看到机器识别博美犬,是真的“看到”了博美的脸,识别轮胎,也是真的”看到“了轮胎。
更高阶的方法是计算gradient,假设原图片为${x_1, \dots, x_n, \dots, x_N }$,对应的loss function值为$e$,改变其中一个pixel,输入为${x_1, \dots, x_n + \Delta x, \dots, x_N }$,此时的loss变为$e + \Delta e$,计算$\mid \frac{\Delta e}{\Delta x} \mid$,即$\mid \frac{\partial e}{\partial x_n} \mid$,该值代表了该pixel的重要程度,画出的图像称为Saliency Map,一些Saliency Map如下。

Saliency Map中的杂讯让整张图不是那么“好看”,一种方法是smooth grad,该方法随机向输入图像添加噪声,得到噪声图像的Saliency Map,并对其进行平均。
要理解机器各层对数据进行了什么处理,一种方法是对输出进行可视化 (高维数据需要降维到2维),另一种方法是Probing (探针),如NLP人物,想分析的层插入一个分类器,如词性分类器,该分类器正确率越高,则该层输出的embedding中包含着词性的信息,需要注意如果本身模型就没有train好,探针的分析结果也是不准确的。
Global Explanation
Global Explanation就是询问机器他认为最像猫咪的图片长什么样子啦,一种方法是在CNN那节提到过的,固定模型参数,寻找使某层输出最大化的输入,按照该种方法找到的输入是AI眼中的世界,也许与我们的认知相差甚远 (如人类看起来像噪声一样的数字图片);另外一种方法是借助Generator如GAN。
首先使用image数据库训练Generator,
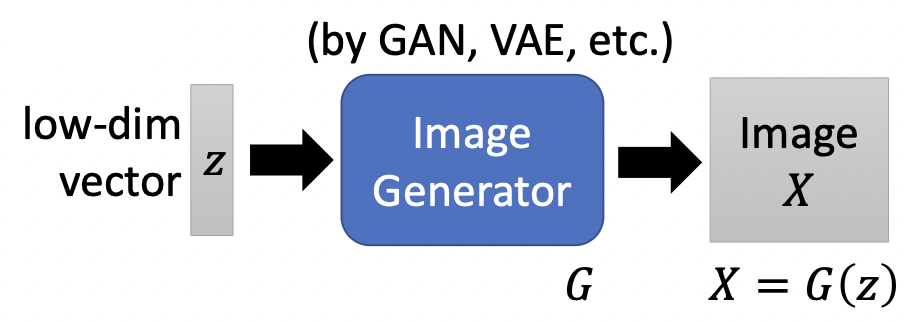
接下来寻找可以使分类器输出最大化的$z^* = \arg \max_z y_i$,对应找到的图片就是$X^* = G(z^*)$,Generator保证了我们找到的图片尽量接近“真实”图片。

除了Local Explanation与Global Explanation,Explainable AI还有许多其他技术,如Local Interpretable Model-Agnostic Explanations (LIME)使用一个Linear Model在一定范围内模拟黑盒模型的输入输出。