Attention and Transformer Networks

Attention的想法源于对人类视觉的研究，当我们看到一副图像的时候，很自然的会对某些部分给予更高的关注

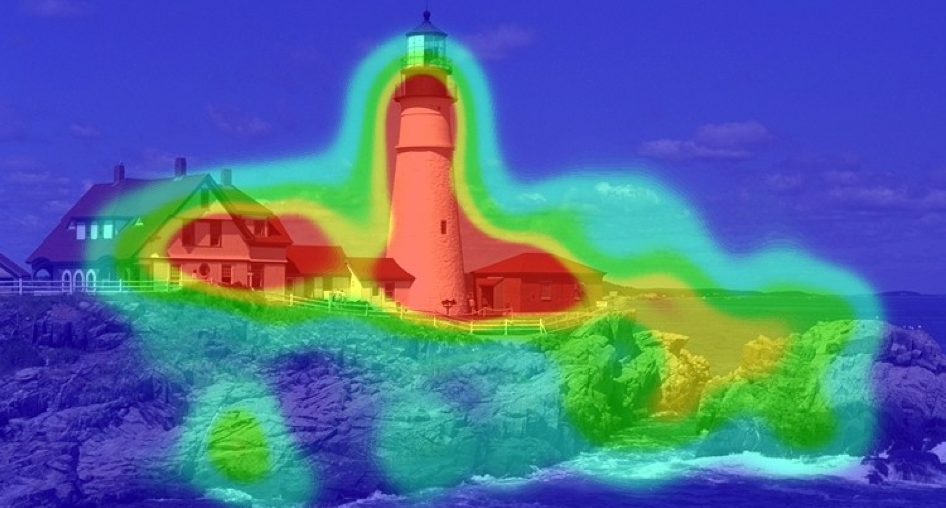
(图源:CS480/680 Lecture 19: Attention and Transformer Networks¹)

在之前的From RNN to Pointer Network，我们讨论了可以处理序列的RNN，他通过将序列循环输入RNN单元，起到“记忆”的作用

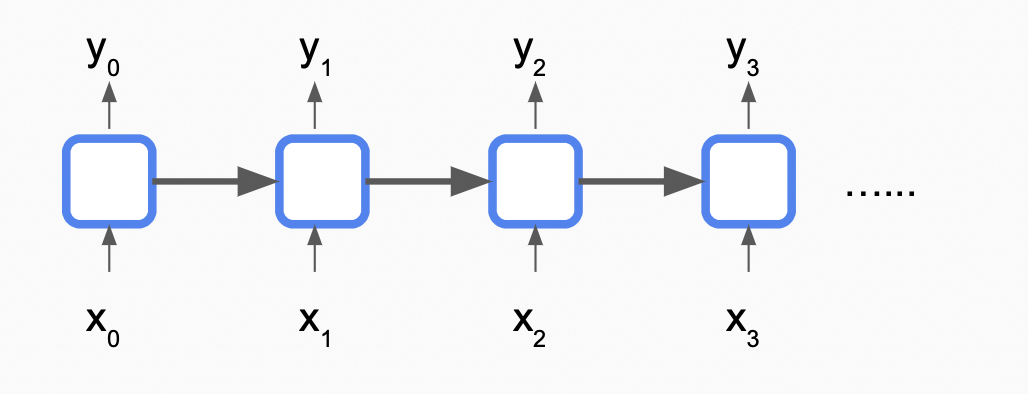
这种设计存在以下几种问题

长期记忆问题，很早之前的输入可能难以起作用
梯度消失和梯度爆炸
网络深度与输入序列成线性关系，难以处理长序列
由于数据是依次输入的，存在顺序关系，难以并行处理，我们的GPU无法起作用

Attention Mechanism

回想数据库查询的过程

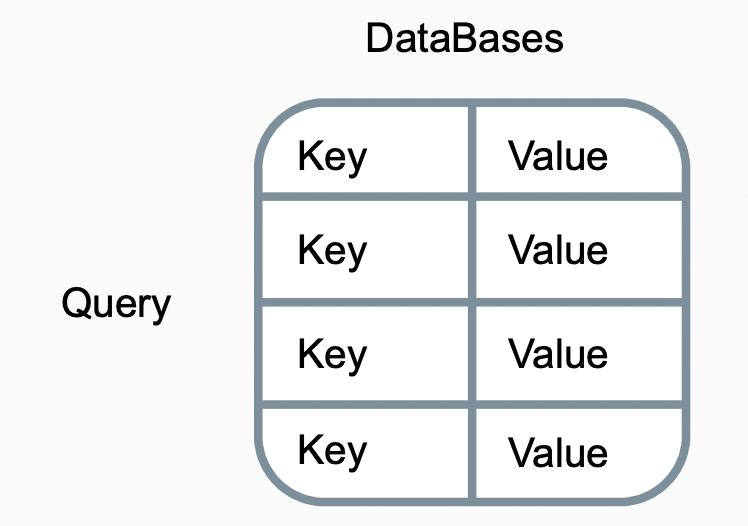
设查询为$q$，键值对为$(k_i, v_i)$，在查询过程中，我们将$q$与所有的$k_i$做比较，最终选出符合查询的$k_i$对应的$v_i$。

Attention以一种类似数据库查询的方式提供了处理序列数据的新思路：

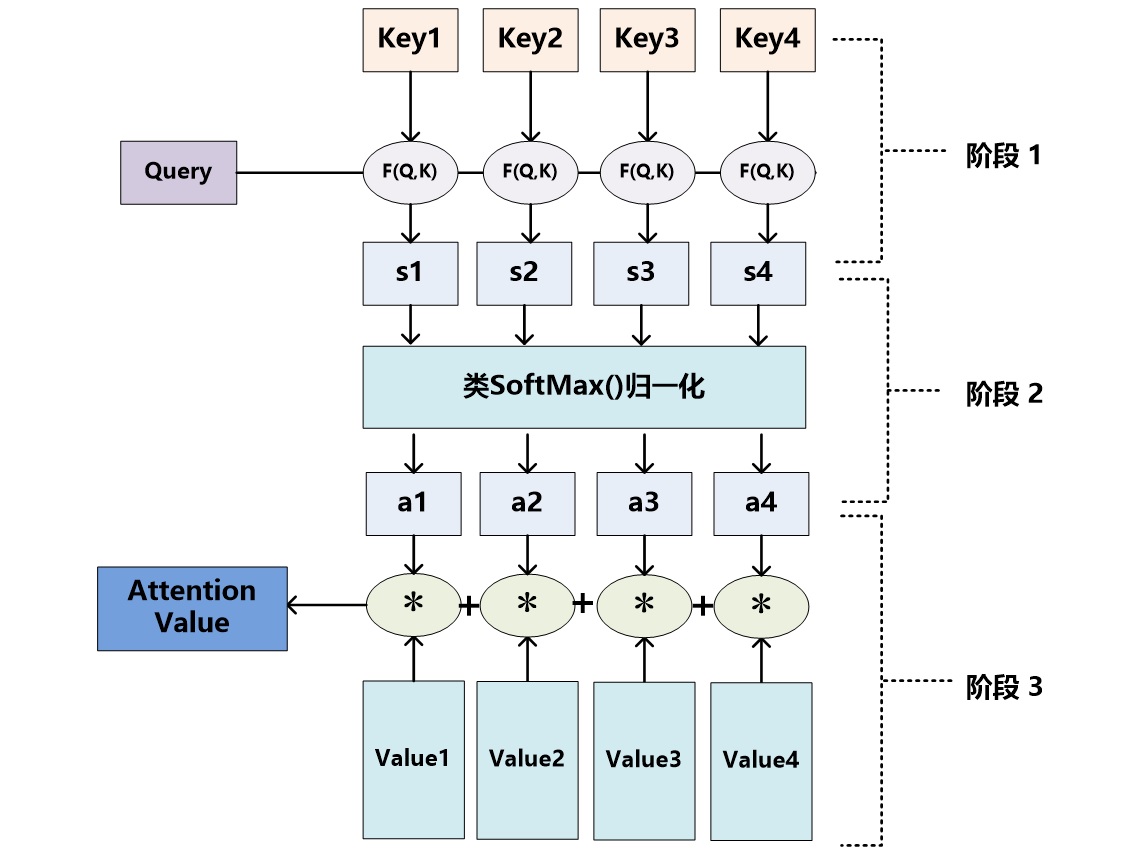
(图源: 深度学习中的注意力机制(2017版)²)

用更形式化的语言描述如下

\[attention(q, \mathbf{k}, \mathbf{v}) = \sum_i softmax(similarity(q, k_i)) \times v_i\]

其中，$attention(q, \mathbf{k}, \mathbf{w})$代表对整个序列的查询结果，$similarity$为标量，代表对查询和键值相似性的评估，评估相似性的方法有许多种：

\[similarity(q, k_i) = \left\{\begin{matrix} q^Tk_i & \text{dot product} \\ \frac{q^Tk_i}{\sqrt{d_{k}} } & \text{scaled dot product}\\ q^TWk_i &\text{general dot product} \\ W^T_q q + W^T_k k_i & \text{additive similarity} \\ \frac{q \cdot k_i}{\left | \right | q \cdot k_i \left | \right | }& \text{cosine similarity} \\ \dots \end{matrix}\right.\]

其中$q^Tk_i$及$\frac{q^Tk_i}{\sqrt{d_{k}} }$设想$q$与$k$在同一空间内，其他的计算方式多是通过线性或非线性方式将$q、k$先映射到新空间，也许在各自的新空间$q、k_i$可以更好的比较，然后在新空间计算相似性。

RNN将序列视为”序列”顺序输入网络，而面对Attention，序列更像“一块”内存：当需要查询的时候，我们以不同的权重一次性访问整个序列；Attention并不存在序列“顺序”输入的问题，也就不存在难以并行，长期记忆，网络深度随序列长度线性增长，梯度等问题。

回忆Attention的三要素：查询，键，值；在翻译任务中，一般有 $\mathbf{k} = \mathbf{v}$，即每个单词本身既作为键又作为值；在self-attention中，一般有 $q \in \mathbf{k}$ ，即对于序列中每个键查询序列其他位置的相关性。

Transformer Network

2015的《Neural Machine Translation by Jointly Learning to Align and Translate》中提出了将Attention用到了NLP领域的翻译任务中。2017年Google Brain团队的《Attention Is All You Need》³，一改翻译任务中用Encoder+Decoder的传统作风，抛弃了RNN/DNN等经典结构，提出了只用Attention机制构成的Transformer模型，模型简单性能又好，这都使Attention在NLP领域得到了更广泛的应用，Transformer结构如下

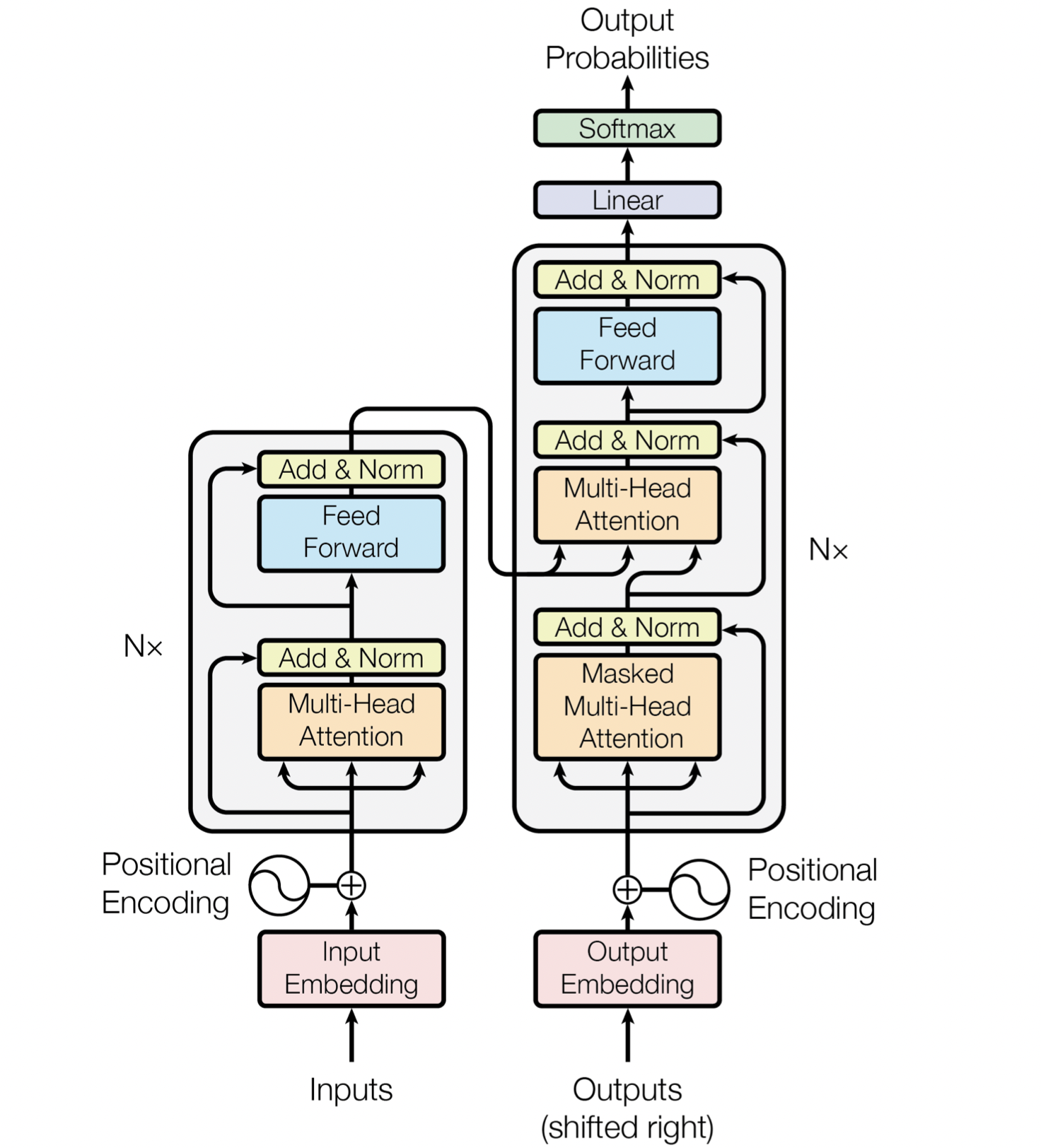
左侧是Encoder部分，我们将整个序列一次性全部输入，编码后经过$N$次MHD以及FF产生最后输出，右侧是Decoder部分，输入的是我们的预期输出序列，与Encoder类似同样要进行编码及添加位置信息，循环$N$次的部分主要包括三层：Masked MHD，MHD，FF，添加一层Masked的原因是，直观来想，在翻译任务中，我们在“产生”一个输出序列的时候，并不应该看到当前输出之后的内容，在MHD层中接收了Encoder部分的输出，类似我们在进行翻译的时候会不时的查看原输入内容。与Encoder不同的是Decoder希望产生一些实际的输出 (如概率) ，为此在其顶部我们添加了 Linear及Softmax层。

让我们逐层了解他们的细节。

Embedding

Embedding层主要作用是将单词映射到某空间内，将单词转变为多维向量，embedding包括词embedding及位置embedding两部分，假设目前输入：“cute cat”。词编码过程如下，最终得到编码矩阵。

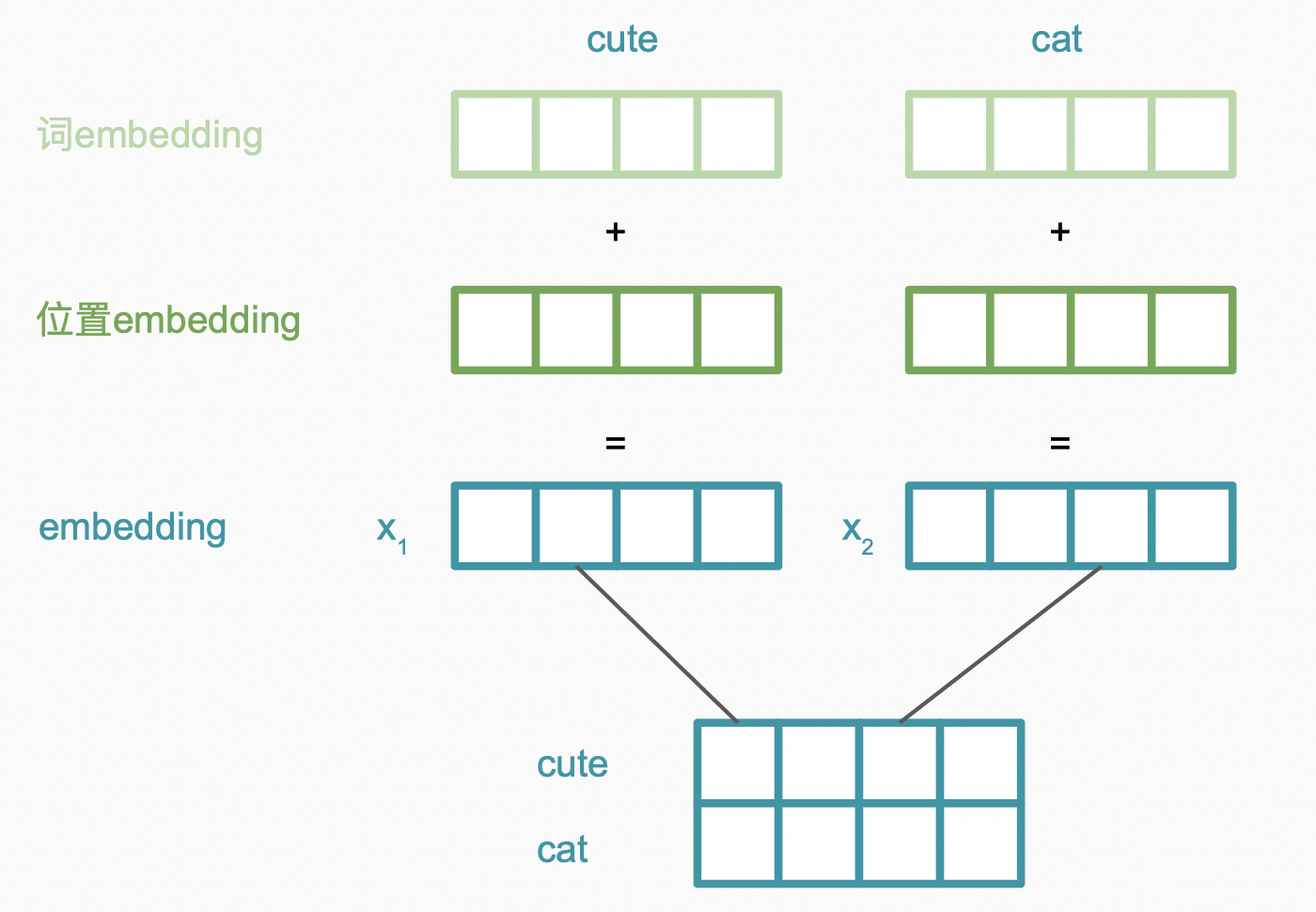
Positional embedding这一步骤是为了将位置信息添加到我们的数据中，弥补我们将序列视为“一块内存”的不足，添加位置有多种方式，如直接将位置附加在原数据后等。为了将位置这一标量展开成向量，以便附加到原数据，Transformer使用了如下的方法。

\[PE_{position,2i} = sin(position/ 10000^{2i/d}) \\ PE_{position,2i+1} = cos(position/10000^{2i/d})\]

Self-attention

回顾attention value的计算过程

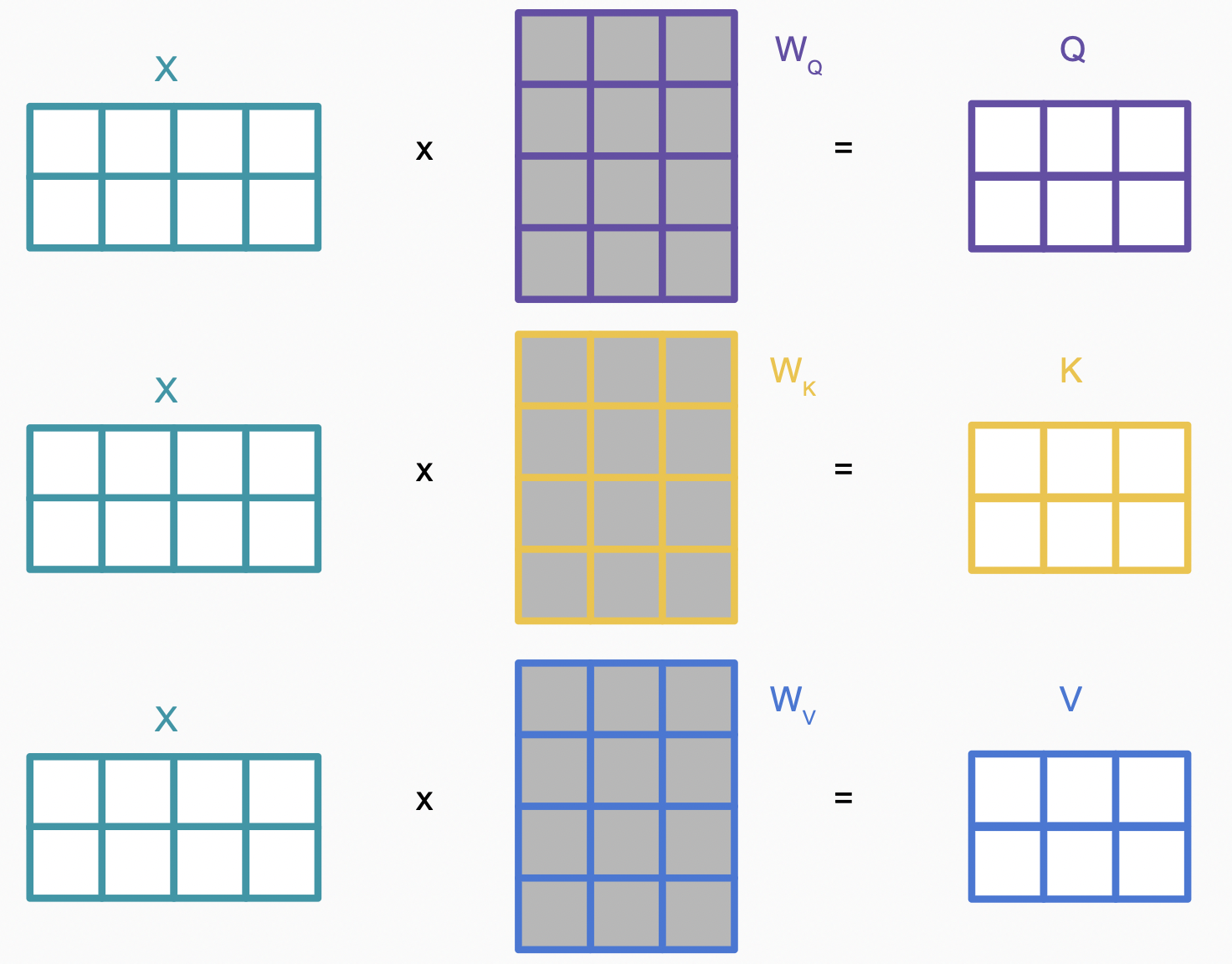
\[attention(q, \mathbf{k}, \mathbf{v}) = \sum_i softmax(similarity(q, k_i)) \times v_i\]

在transformer中的self-attention中，$q$，$k_i$， $v_i$都是输入$x_i$的不同线性变换 ($W_Q, W_K, W_V$)，以$q$的计算为例

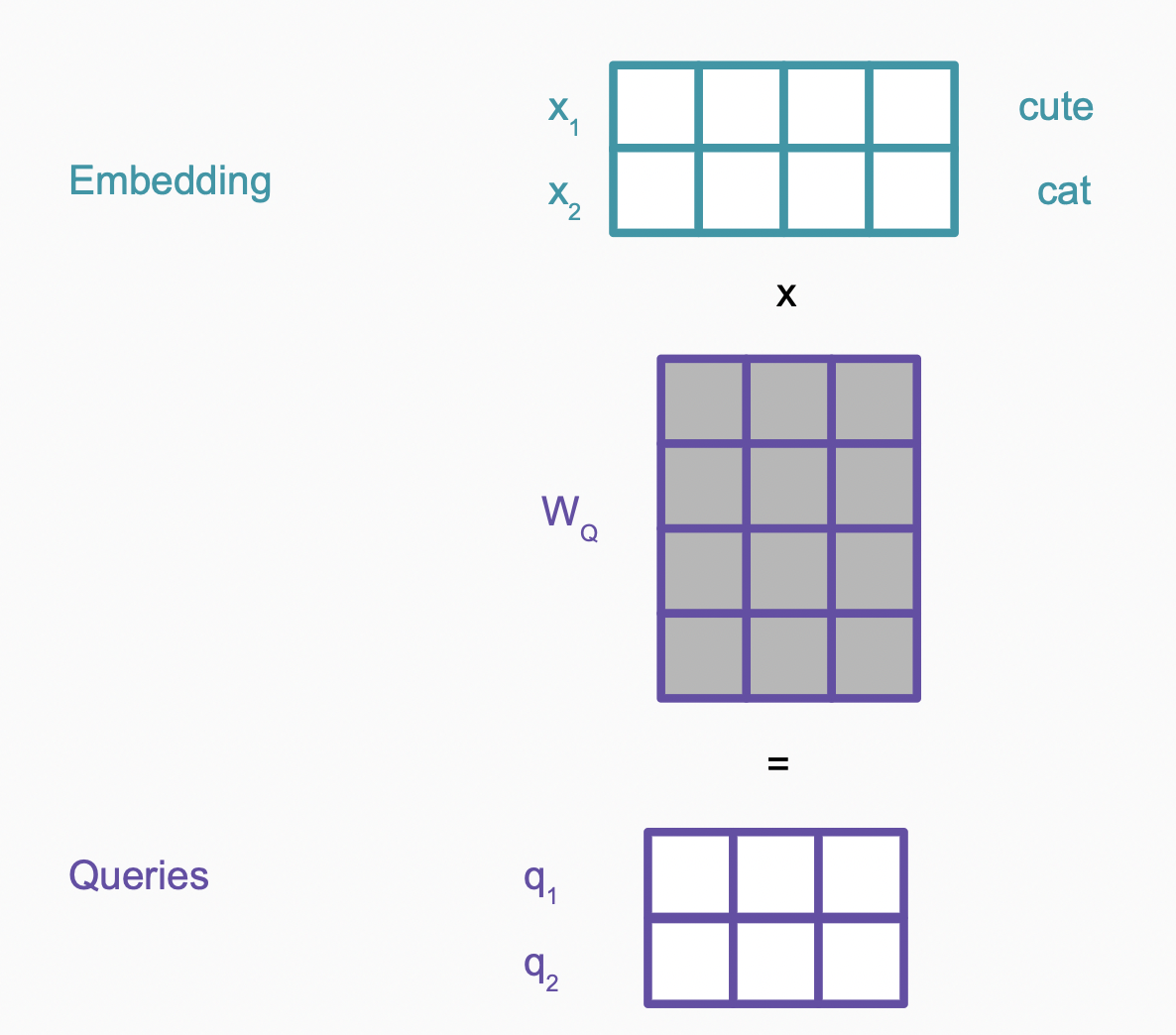
经过Linear层得到$Q,K,V$，接下来计算$similarity(q, k_i)$，上文中我们提到有多种计算方法，以$\text{scaled dot product}$为例，$similarity(q, k_i) = \frac{q^Tk_i}{\sqrt{d_{k}} }$。

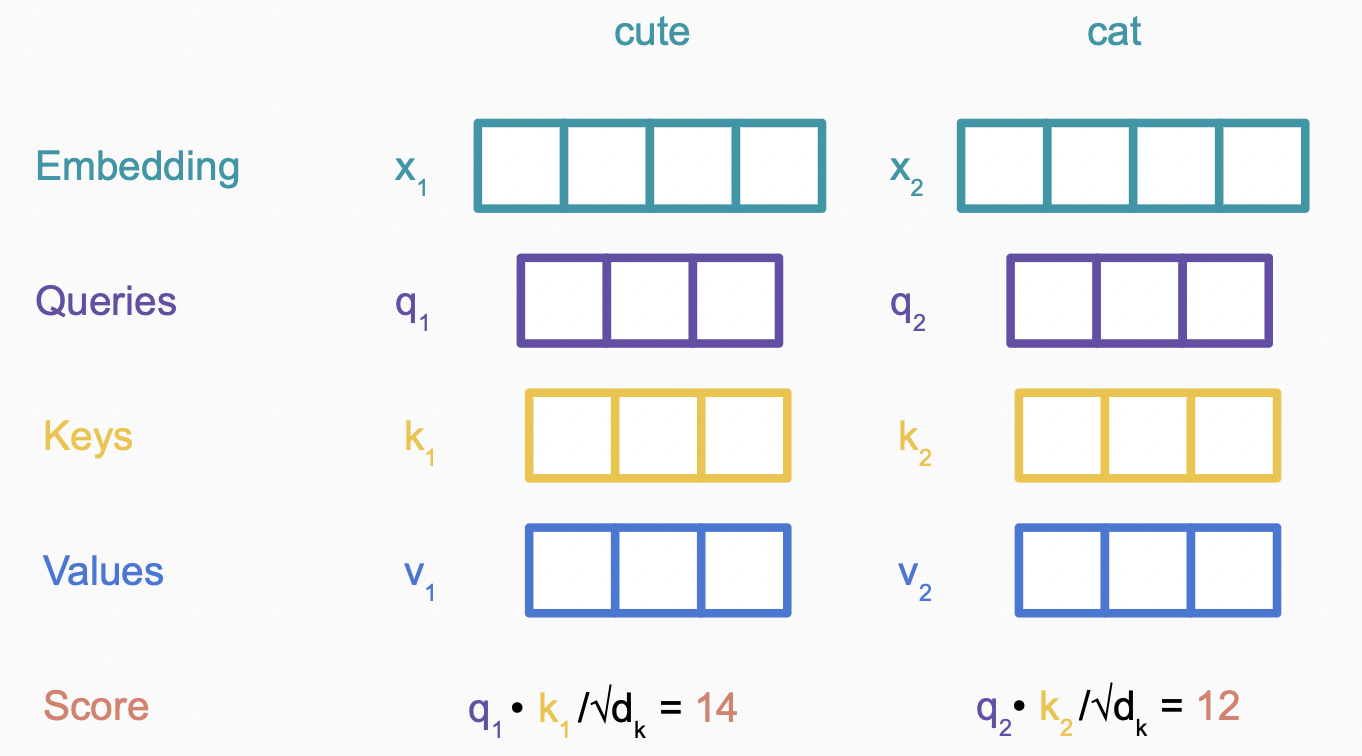
$similarity$再经过$softmax$，加权和，就得到该次的查询结果，以计算”cute”的attention value为例

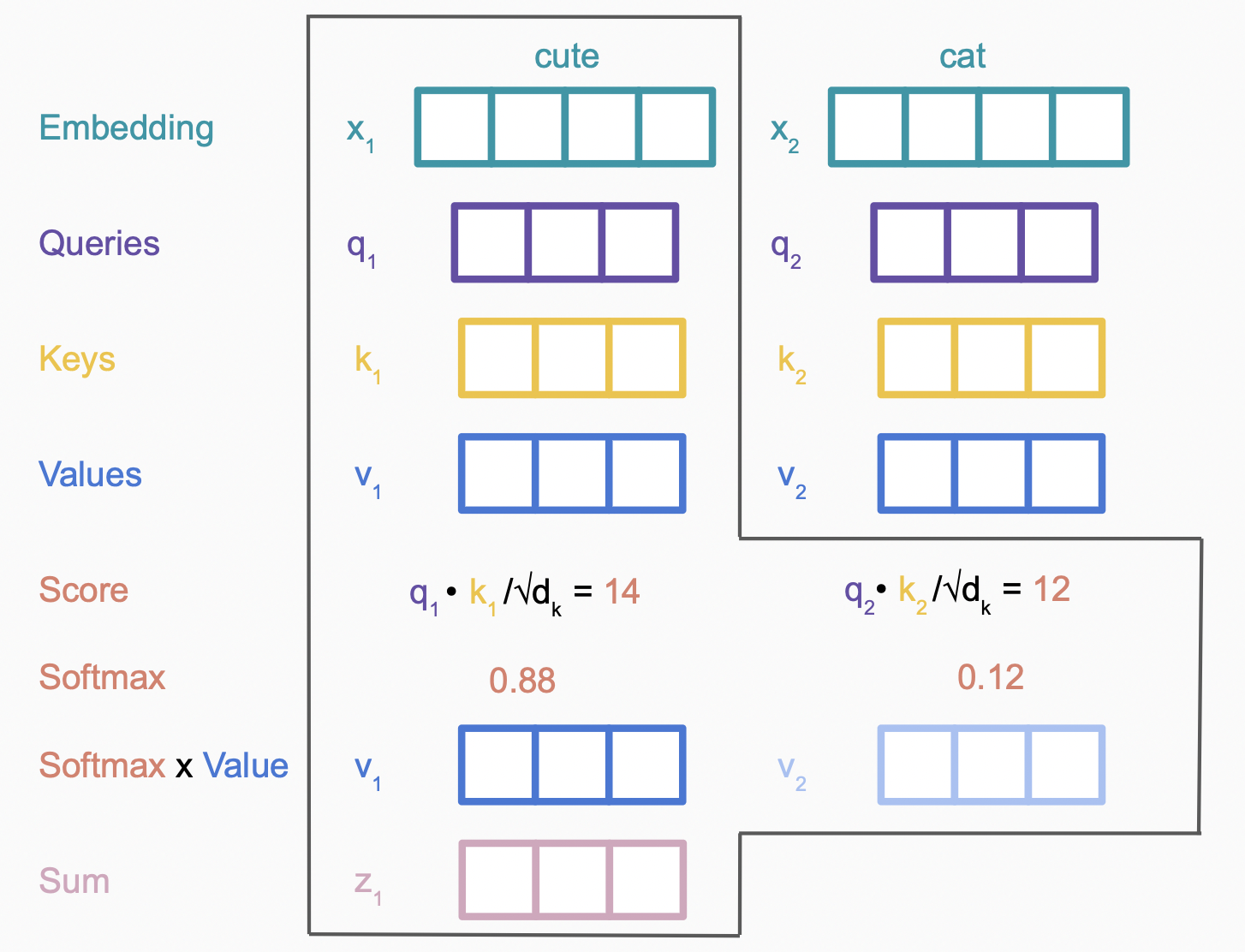
将以上运算放到整个矩阵中看，如下

Multi-head attention

在MHD层中使用的是self-attention，$q \in \mathbf{k} , \ \mathbf{k} = \mathbf{v}$，该层结构抽象化如下：

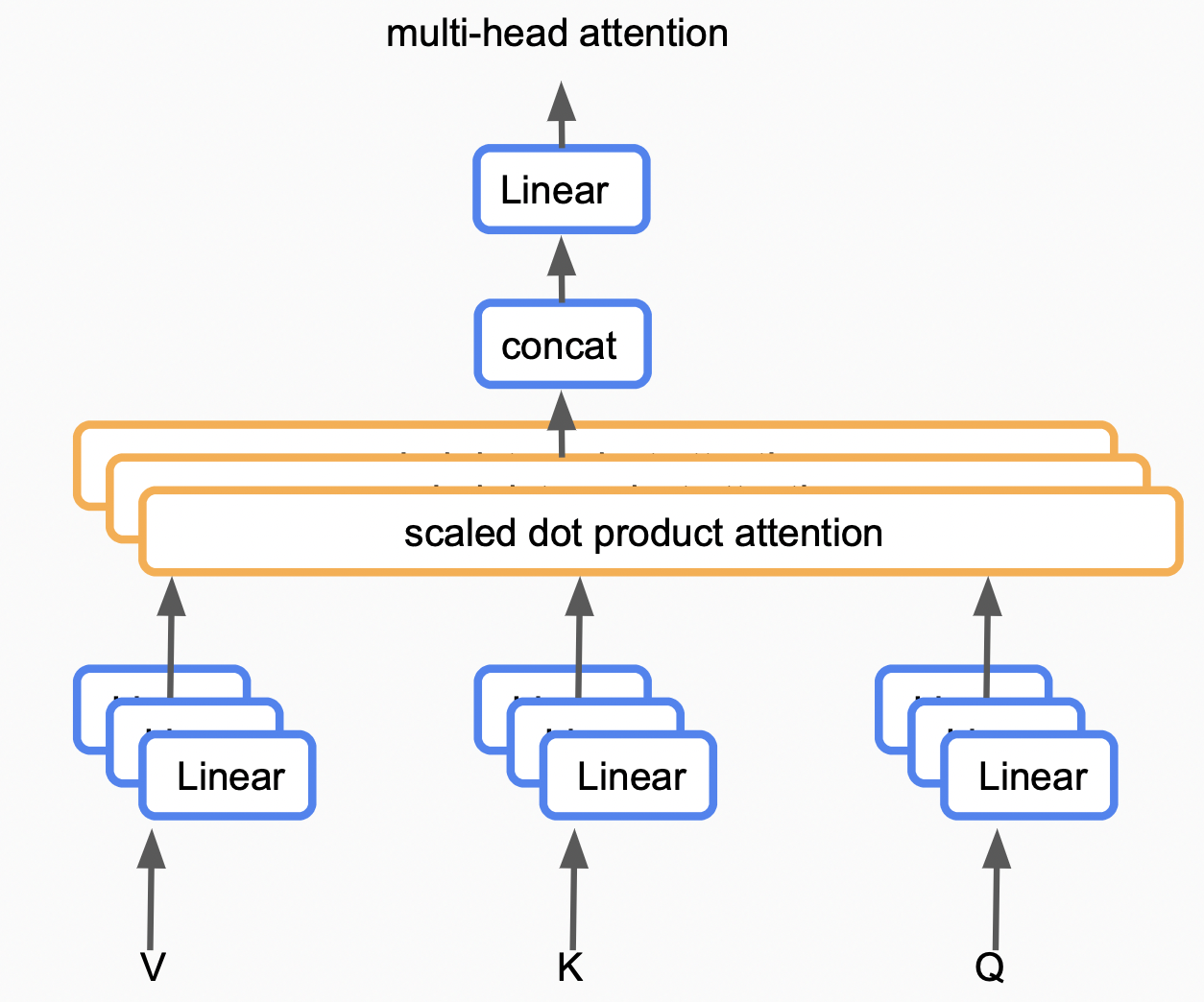
源序列同时作为$V、K、Q$输入，首先经过一个多层Linear，该部分将输入映射到多个空间中，在以后我们会在不同的空间进行attention value的计算；

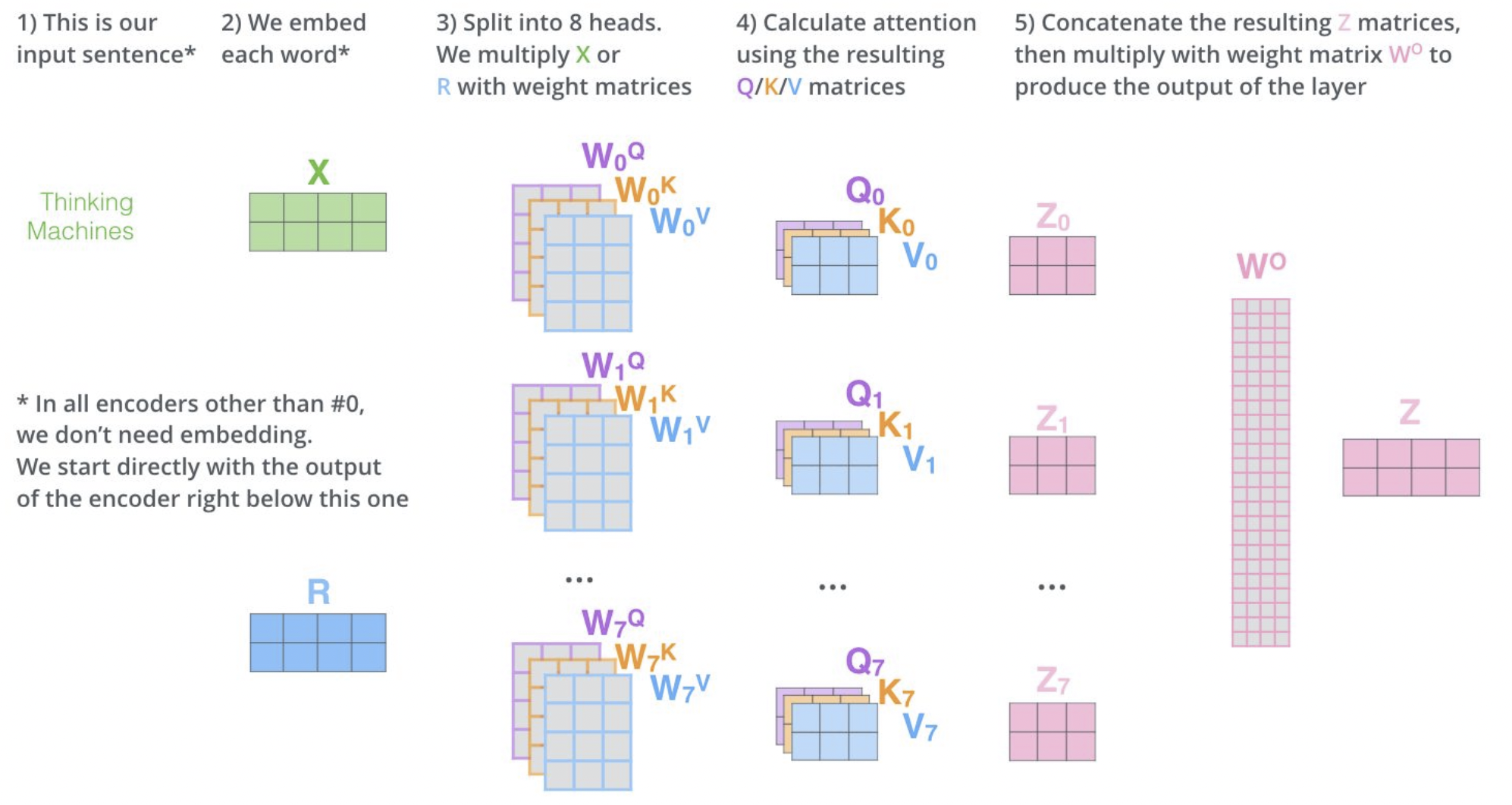
最后将各空间中采集到的attention value进行Concat，Linear后得到multi-head attention。

在Transformer中，MHD层循环了$N$次；在循环一次时，输出的是原序列中每元素对其他元素的attention value，循环两次时，查询attention value的attention value，即多对多的查询，循环$N$次的目的即是我们不止想查询一对元素之间的关系，而是想查询一组元素和另一组元素之间的关系。

MHD层另外添加了残差连接及Normalization，残差连接使得最后的输出不仅包括每个位置对应查询出的所有单词，也包括原始该位置的单词。

MHD的计算过程格式化描述如下：

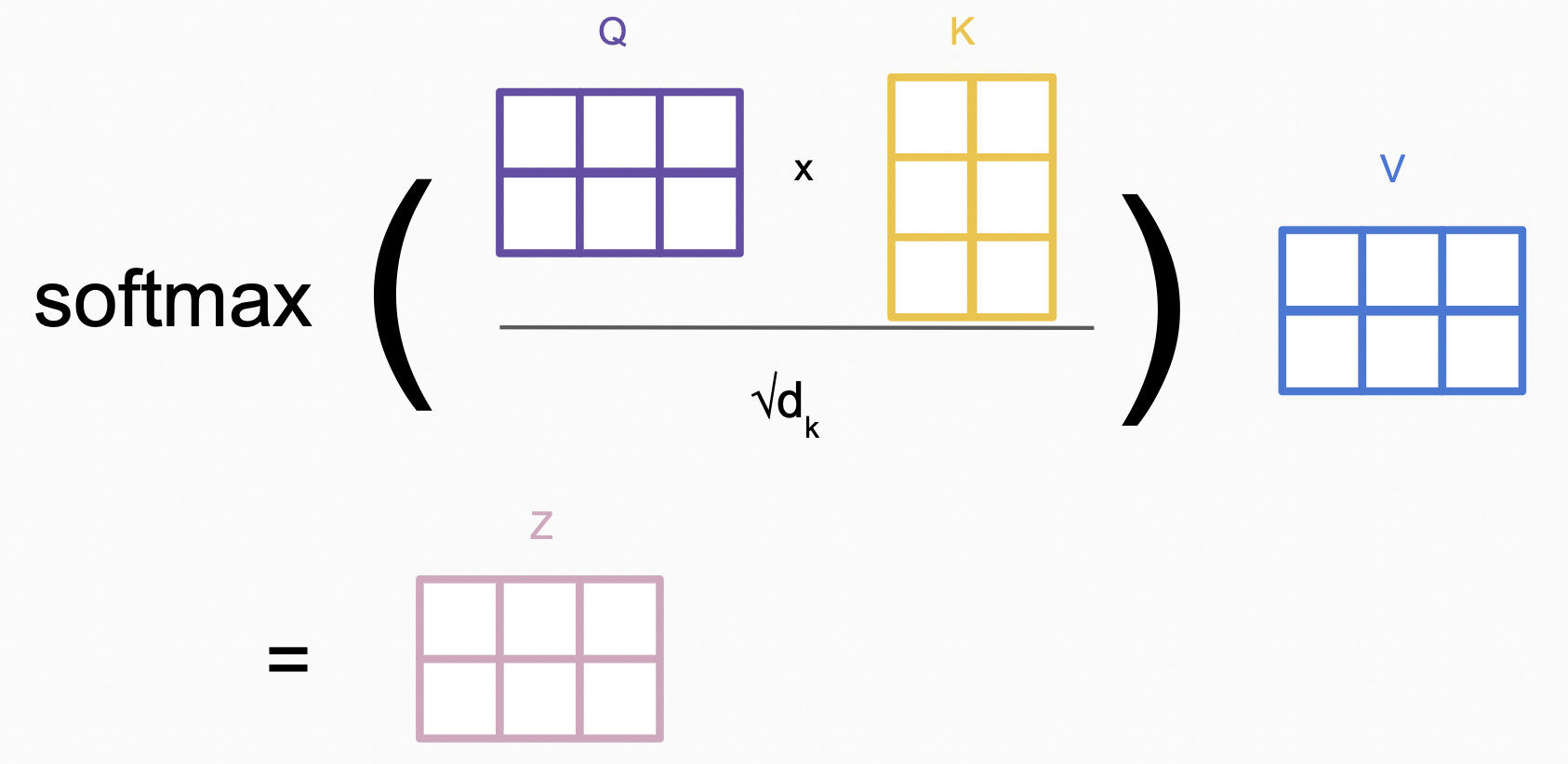
\[multihead(Q,K,V) = W^Oconcat(head_1, head_2, \dots, head_h) \\ head_i = attention(W_i^Q Q, W_i^K K, W_i^V V) \\ attention(Q, K, V) = softmax \Big(\frac{Q^T K}{\sqrt{d_k}} \Big) V\]

Layer Normalization

Normalization层的添加可以有效减少梯度下降所需的步数。举例来说，如果$x$是二维向量：$w、b$，$b$维度方差远大于$w$维度，损失函数为$J$，则有函数图像如下

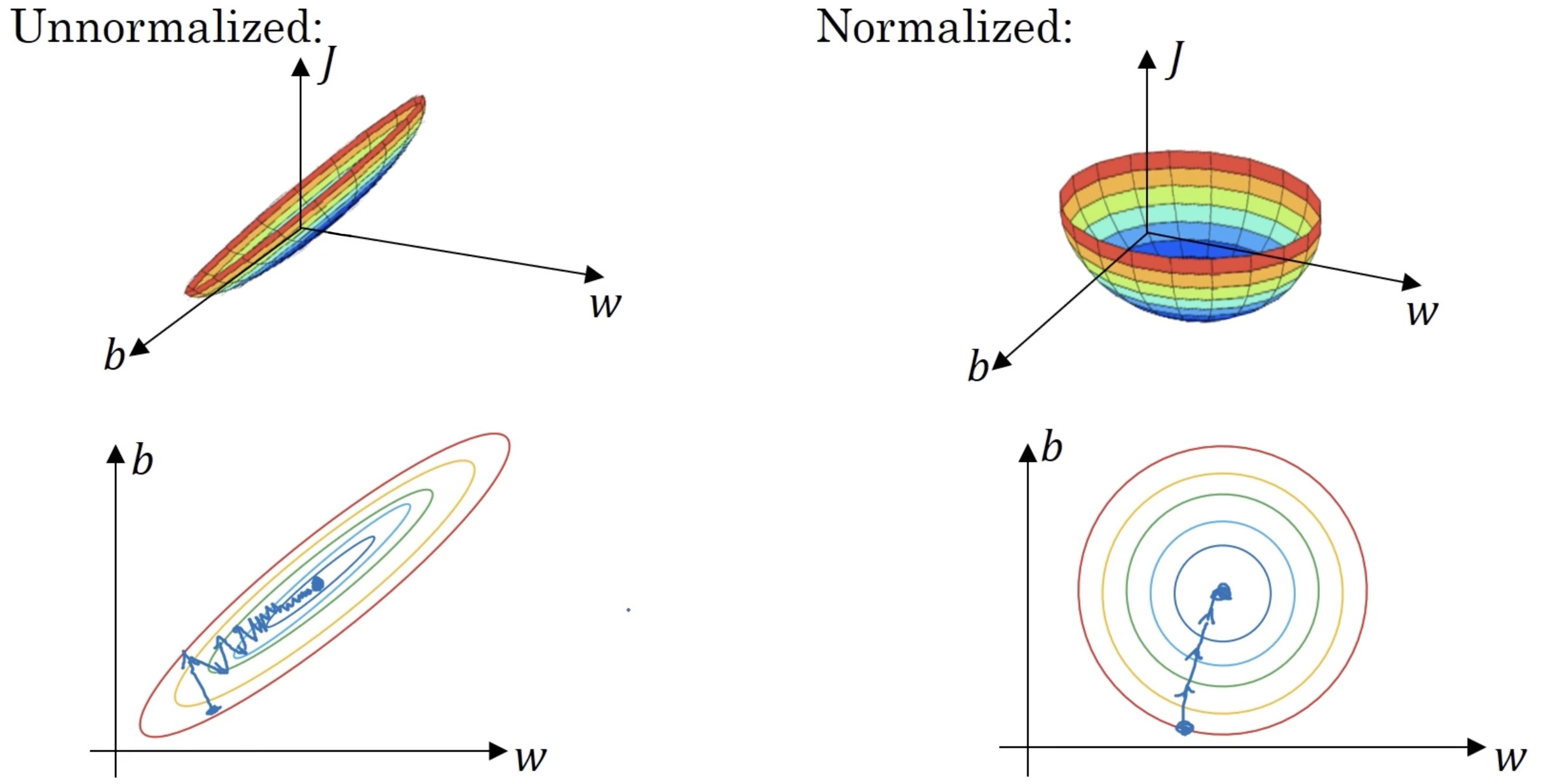
(图源Normalizing Inputs (C2W1L09) by DeepMind)

注意图中梯度下降的标线，可以看到未Normalization的情况下，由于$b$维度方差更大，在降低梯度方面占据更多的”权重”，我们会尝试先尽快在维度$b$方向上移动，最终经历多次颠簸最终才达到目的地。

设隐藏层单元为$h_i$，则Normalization公式如下

\[h_i \gets \frac{g}{\sigma}(h_i - \mu ) \\ g \text{ is a variabe, }\ \mu = \frac{1}{H} \sum_{i=1}^{H}h_i \ ,\ \sigma = \sqrt{\frac{1}{H} \sum_{i=1}^{H}(h_i - \mu)^2}\]

Masked Multi-head attention

在Decoder中，序列首先经过了Masked MHD，直观来想，在翻译任务中，我们在“产生”一个输出序列的时候，并不应该看到当前输出之后的内容 (认为未来的输出还没产生)，即需要屏蔽“未来”的单词。

在这里另外一个小Tip是我们需要在$softmax$之前做好屏蔽的操作，以便$softmax$之后我们仍然可以得到总和为1的概率。

\[maskedAttention(Q, K, V) = softmax \Big(\frac{Q^T K + M}{\sqrt{d_k}} \Big) V \\ \text{where M is a mask matrix of }0's\text{ and }-\infty's\]

Others

Transformer是一类不依赖于递归的序列神经网络的起点，在这之后人们发明出许多基于此结构的优秀的神经网络，如GPT，BERT等，他们均在NLP领域取得了突破性进展，我们将在其他文章了解他们。

CS480/680 Lecture 19: Attention and Transformer Networks - Jul 17, 2019 by Pascal Poupart on Youtube ↩︎
深度学习中的注意力机制(2017版) - Dec 10, 2017 by 张俊林 ↩︎
Vaswani, Ashish, et al. “Attention is all you need.” Advances in neural information processing systems. 2017. ↩︎