Markov Decision Processes
MDP问题
在学习一些算法如状压DP时,有这样的思想:目标解存在于状态空间中,我们从目前的“状态”,做出一定的“动作”,转移到下一个状态,直到搜到我们希望的最终解。

考虑电车问题:
$n$ 个节点编号 1 ~ $n$,某时刻选择走路将从 $s$ 到 $s+1$ 并花费1 mins,选择坐电车将从 $s$ 到 $2s$ 并花费 2 mins;
如何用最短的时间从 $1$ 到 $n$ ?
在这类搜索问题中,我们做出“动作”,得到的“状态”、“奖励”等是确定的:我们在$s$选择做电车,一定会花费2 mins,并得到状态$2s$。对这类“确定”的问题,我们可以在搜索空间进行搜索,最终找到一系列的“动作”(如:走路 - 电车 - 电车 - 电车 - 走路)作为我们的目标解。
Markov Decision Processes (MDP)在上面问题的基础上,引入了不确定性:做出一个动作,但这个动作不是转移到下一个状态,而是以多种概率转移到多个状态。
$n$ 个节点编号 1 ~ $n$,某时刻选择走路将从 $s$ 到 $s+1$ 并花费1 mins,选择坐电车将花费2mins,有$0.5$的可能从 $s$ 到 $2s$,有0.5的可能留在原地;
如何用最短的时间从 $1$ 到 $n$ ?
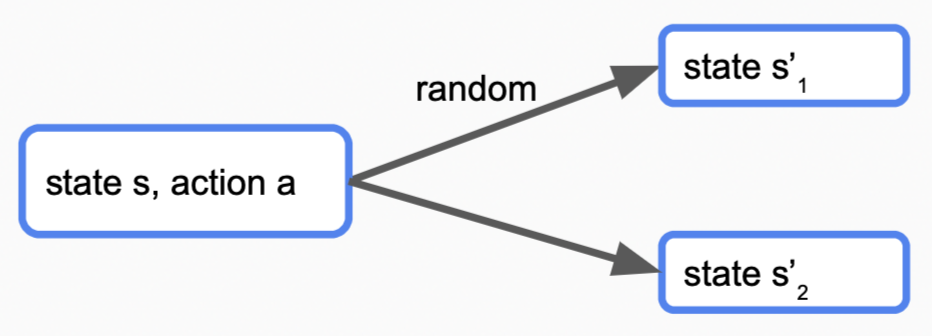
对于该类问题,形式化的表述如下:
\[\begin{align} & States: \text{可能的states集合} \notag \\ & s_{state} \in States: \text{初态} \notag \\ & Actions(s): \text{状态s可能的动作a集合} \notag \\ & T(s, a, s'): \text{在状态s做出a之后到达}s'\text{的概率} \notag \\ & Reward(s, a, s'): \text{在状态s做出a之后到达}s'\text{的收益} \notag \\ & IsEnd(s): 状态s是否为终态 \notag \\ & \gamma \in [0,1]: \text{未来奖励衰减系数discount factor, 默认为1} \notag \end{align}\]$关于\gamma$的具体概念将在后面展开。
为了展示状态之间的转移关系,引入choice node的概念:在状态$s$,选择动作$a \in Action(s)$将转移到一个$\text{choice node}(s, a)$,该node有一至多条出边,每条边有两个值:$T(s, a, s’)$及$Reward(s, a, s’)$代表走该条边的概率以及获得的reward。考虑以下赌钱问题:
初态in,末态end,在每一步你有两种操作可选:stay继续游戏,有0.6的概率继续游戏并得到4¥,有0.4的概率结束游戏并得到5¥,quit结束游戏,有1的概率结束游戏并得到10¥;
如何得到尽可能多的钱币?
对该问题的状态转移关系可视化即为:
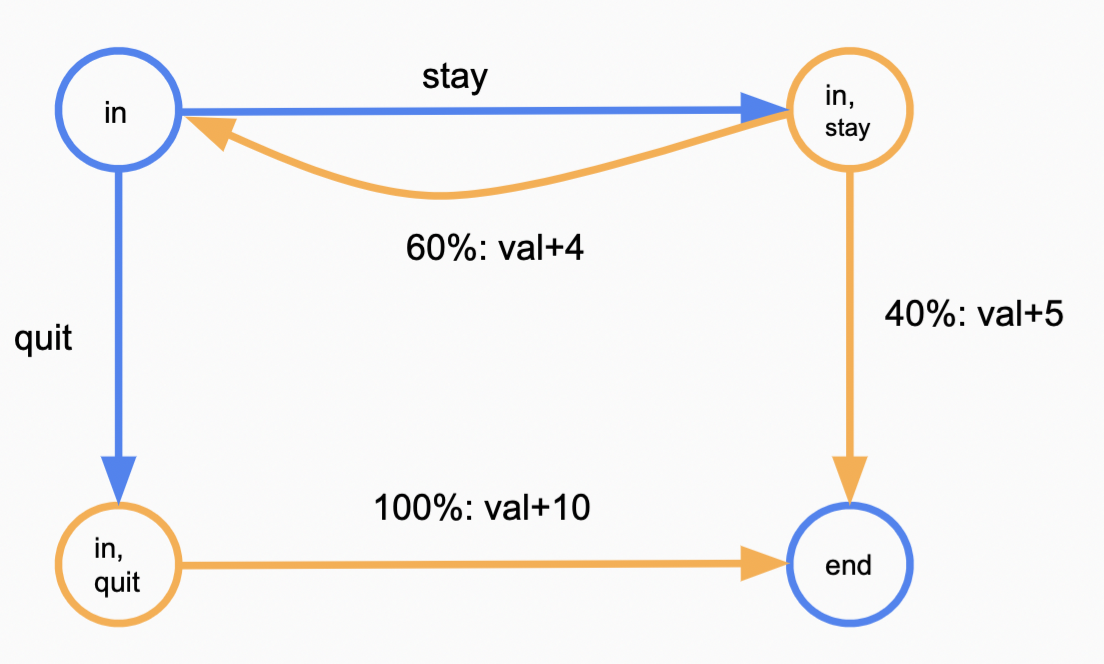
上图中,蓝色节点代表状态节点$s$,引出的蓝色边代表做出的动作$a$,橘色代表choice node,引出的橘色边代表$s,a$可能的转移;在in状态,选择动作stay将转移到概率节点(in, stay),该节点展示有 $T(in, stay, in)$ = 0.6的概率到达状态节点in,并获$Reward(in, stay, in)$ = 4,有 $T(in, stay, end)$ = 0.4的概率转移到end终态,并获得 $Reward(in, stay, in)$ = 5。
解的形式
对于确定性问题,最终解为一个最终的答案序列 (如走路 - 电车 - 电车 - 电车 - 走路);当面对MDP问题时,情况可能更复杂一些,我们需要的解不再是一个序列,而是一组策略 $\pi $ : $s \Rightarrow a$的映射,其中 $s \in States$,$a \in Action(s)$ 。即对于每一个状态$s$,我们可以使用$\pi(s)$指该步的动作。

求解
对于一个状态-动作path:$s_0, a_1r_1s_1, a_2r_2s_2, \dots $,其中$s$代表状态,$r$代表收益,在状态$s_0$时认为path总收益 (utility) 是由以下迭代式得到的:
\[\begin{align} u_1 & = r_1 + \gamma u_2 \notag \\ u_2 & = r_2 + \gamma u_3 \notag \\ & \dots \notag \end{align}\]即$u_1 = r_1 + \gamma r_2 + \gamma ^2 r_3 + \gamma ^3 r_4 +\dots$
可以看到,我们不是做简单的累加 $\sum$ ,而是增加了一个影响因子 $\gamma$ ,其代表我们对“未来”赋予的影响度。当$\gamma = 1$时,代表我们认为未来与现在同样重要,当$\gamma = 0$时,代表我们只关注于现在。后文中可以看到,当MDP图存在环时,$\gamma$ 的增加对保持算法收同样是有收敛性的。
当位于状态$s$时,对于策略$\pi(s)$,由于不确定性$\pi(s)$将引出许多path

定义$V_\pi(s)$为从$s$状态开始执行策略$\pi(s)$的期望收益,$Q_\pi(s, a)$为概率节点$(s, a)$的期望收益,即多个path的utility期望值。
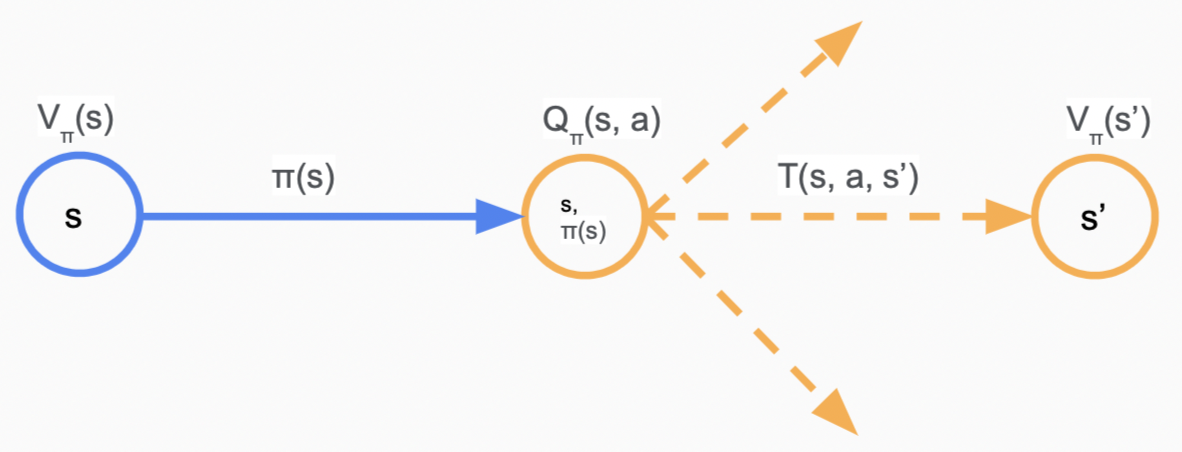
可以得出以下的等式(Bellman, 1957):
\[V_\pi(s) = \begin{cases} 0 & \text{if } IsEnd(s)= True\\ Q_\pi(s, \pi(s)) & otherwise. \end{cases} \\ Q_\pi(s, a) = \sum_{s'} T(s, a, s')[R(s, a, s') + \gamma V_\pi(s')]\]以上面提到的赌钱游戏为例,设$\gamma = 1$,$\pi(in) = stay$
\[\begin{align} V_{\pi}(end) & = 0 \notag \\ V_{\pi}(in) & = Q_\pi(in, stay) = 0.4 * (5 + V_{\pi}(end)) + 0.6 * (4 + V_{\pi}(end)) \notag \\ & = 6.5 \notag \end{align}\]当面对更复杂的情况时,我们可以用下面的算法 (Policy Evaluation) 求解
${\color[RGB]{159,46,39}{\text{Algorithm: policy evaluation}}}$
\[\begin{align} & \text{对于所有状态}s\text{, 初始化}V_\pi^{(0)}(s) \gets 0 \notag \\ & for\ t = 1, \dots,t_{PE}: \notag \\ & \ \ \ \ for\ each\ state\ s: \notag \\ & \ \ \ \ \ \ \ \ \ \ \ V_\pi^{(t)}(s) \gets \ Q_\pi^{(t-1)}(s, a) = \sum_{s'} T(s, a, s')[R(s, a, s') + \gamma V_\pi^{(t-1)}(s')] \notag \end{align}\]
其中,$t_{PE}$代表迭代次数,由自定的阈值决定:
\[max_{s \in States} |V_\pi^{(t)}(s) - V_\pi^{(t-1)}(s)| \le \epsilon\]以上的计算是在我们已经有一个策略$\pi(s)$的情况下进行的,如果现在策略未知,要求最大收益$V_{opt}(s)$,自然而然可以想到通过循环计算每个可能的$Q_\pi(s, a)$,最终取$max$ 。
定义$V_{opt}(s)$为从$s$状态开始的最大期望收益,$Q_{opt}(s, a)$为概率节点$(s, a)$的最大期望收益,有
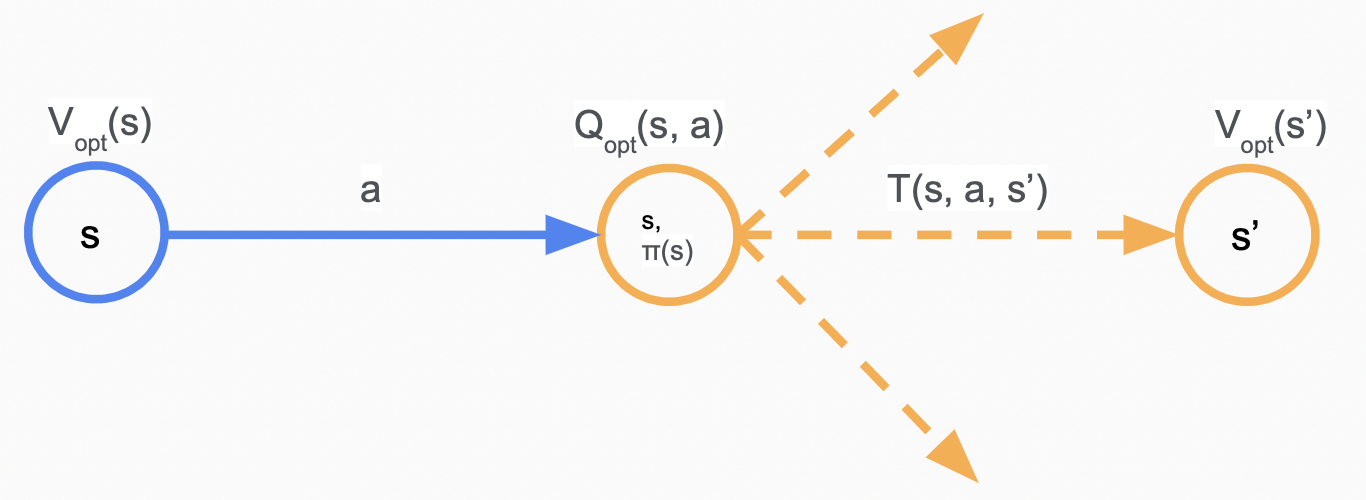
至此,根据对策略$\pi(s)$收益的定义,可以得知最优解为
\[\pi_{opt}(s) = \text{argmax}_{a\in Actions(s)}Q_{opt}(s, a)\]通过与下面的算法,我们可以求得未知策略情况下的最大期望收益 (Value Iteration):
${\color[RGB]{159,46,39}{\text{Algorithm: value iteration}}}$
\[\begin{align} & \text{对于所有状态}s\text{, 初始化}V_{opt}^{(0)}(s) \gets 0 \notag \\ & for\ t = 1, \dots,t_{VI}: \notag \\ & \ \ \ \ for\ each\ state\ s: \notag \\ & \ \ \ \ \ \ \ \ \ \ \ V_{opt}^{(t)}(s) \gets {\color{Red}{max_{a \in Action(s)}} } \ Q_{opt}^{(t-1)}(s, a) \notag \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \gets {\color{Red}{max_{a \in Action(s)}} } \ \sum_{s'} T(s, a, s')[R(s, a, s') + \gamma V_{opt}^{(t-1)}(s')] \notag \end{align}\]
其中,$t_{VI}$代表迭代次数,由自定的阈值决定。
收敛性
当$\gamma < 1$或MDP图无环时,显然Value Iteration是收敛的。
Reinforcement Learning
再次回顾MDP问题的形式化表述:
\[\begin{align} & States: \text{可能的states集合} \notag \\ & s_{state} \in States: \text{初态} \notag \\ & Actions(s): \text{状态s可能的动作a集合} \notag \\ & {\color{Red}{T(s, a, s')} }: \text{在状态s做出a之后到达}s'\text{的概率} \notag \\ & {\color{Red}{Reward(s, a, s')} }: \text{在状态s做出a之后到达}s'\text{的收益} \notag \\ & IsEnd(s): 状态s是否为终态 \notag \\ & \gamma \in [0,1]: \text{未来奖励衰减系数discount factor, 默认为1} \notag \end{align}\]对MDP过程,我们知道世界是如何运行的:知道做出动作之后的状态的转移概率$T(s, a, s’)$,知道做出动作并转移的收益$Reward(s, a, s’)$。Reinforcement Learning (RL)更像一个未知的环境:
\[\begin{align} & States: \text{可能的states集合} \notag \\ & s_{state} \in States: \text{初态} \notag \\ & Actions(s): \text{状态s可能的动作a集合} \notag \\ & IsEnd(s): 状态s是否为终态 \notag \\ & \gamma \in [0,1]: \text{未来奖励衰减系数discount factor, 默认为1} \notag \end{align}\]为了获得关于环境的信息,我们的代理 (agent) 需要主动的做出一些动作,获得环境 (environment) 对我们的反馈,继续进行下一次动作
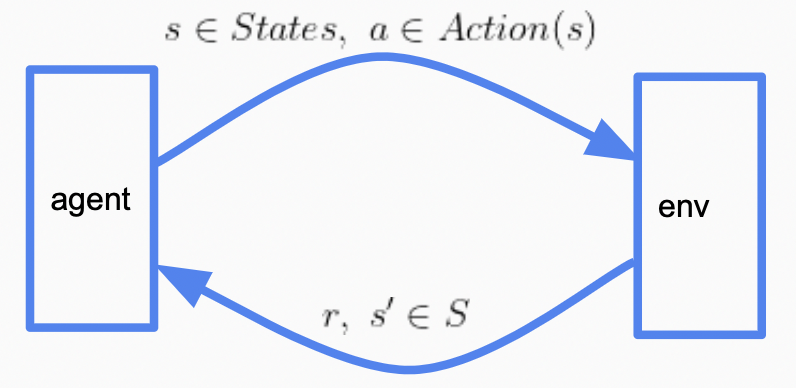
Monte-Carlo methods
借鉴在Markov Decision Processes一节中提到的求解MDP的方法,面对RL问题时候,我们可以通过主动探索得到的数据估计我们的$T(s, a, s’)$、$Reward(s, a, s’)$,即基于模型的蒙特卡洛方法:先估计MDP模型,再通过Value Iteration求解MDP。
其中$#$代表某种计数值。
考虑上文提到过的赌钱游戏
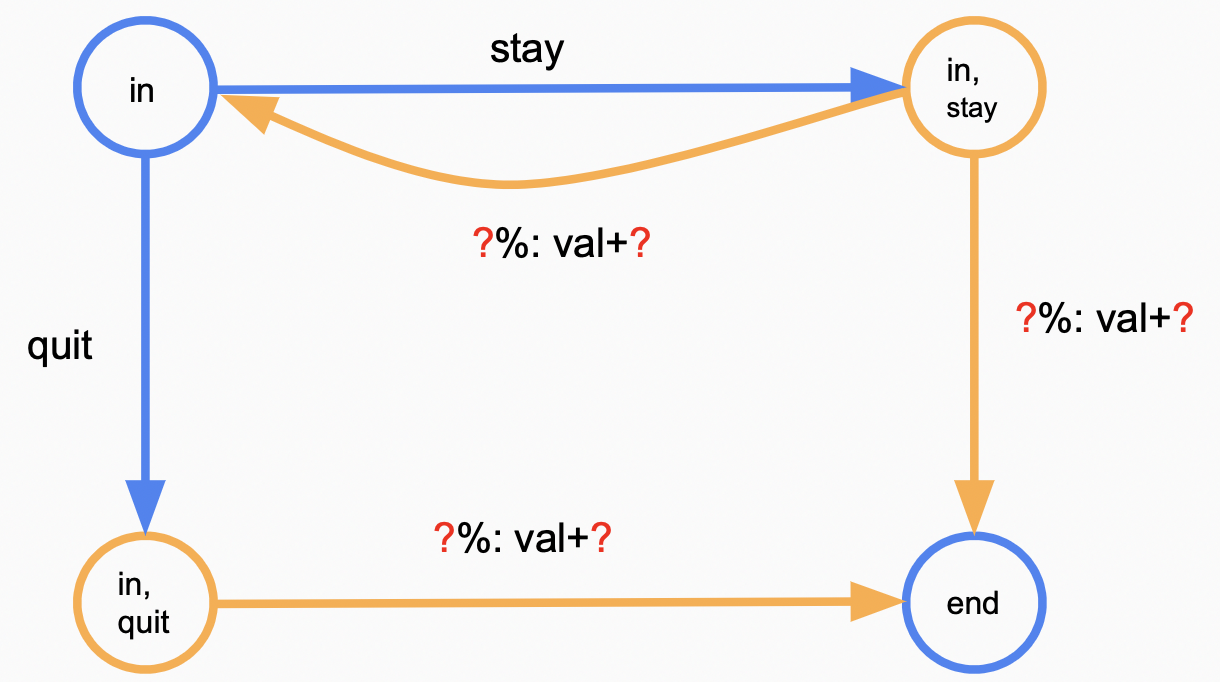
假设遵循策略$\pi$,我们有如下一些探索序列 (${\color{RED}{s_0}};a_1, r_1, {\color{RED}{s_1}};a_2, r_2, {\color{RED}{s_2}};\dots; a_n, r_n, {\color{RED}{s_n}}$):
[in; stay, 4, end]
[in; stay, 4, in; stay, 4, end]
[in; stay, 4, in; stay, 4, in; stay, 4, in; stay, 4, end]
那么我们可以有如下的估计
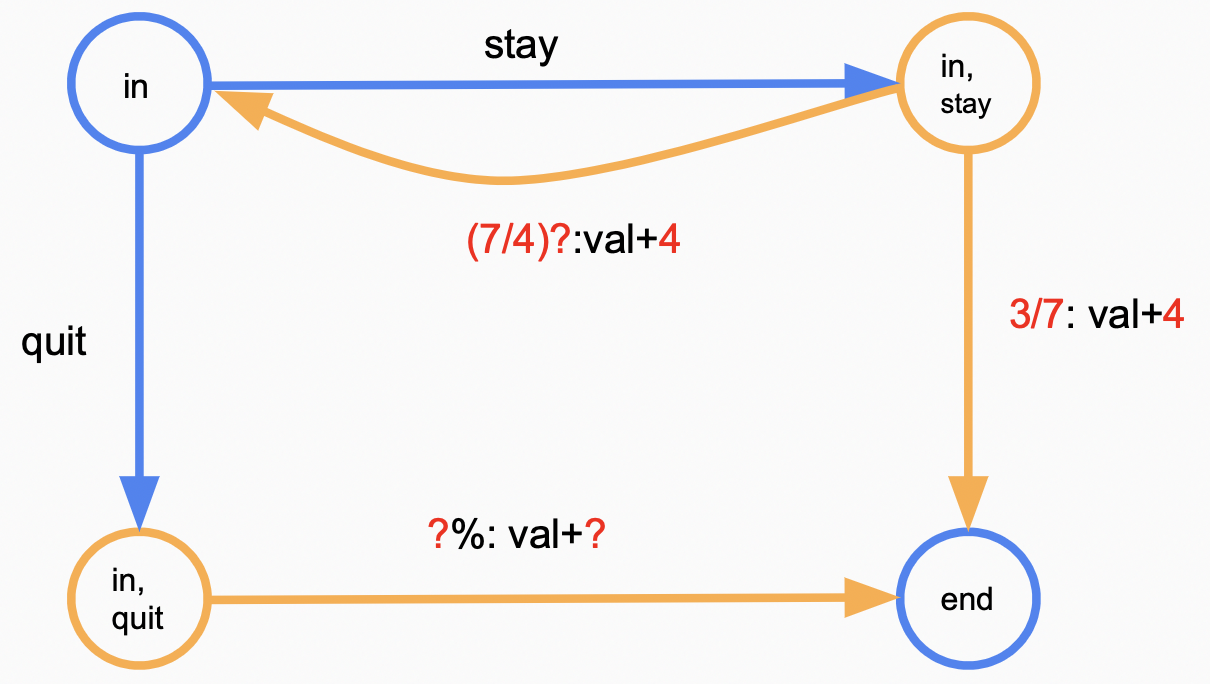
目前为止可以看到一个明显的问题:如果$s \neq \pi(s)$,我们永远无法到达$(s, a)$ ;就上面的序列来说,我们无法预估$\hat{Q}_\pi(in, quit)$ 。同其他机器学习不同,强化学习的“探索”显得尤为重要:强化学习需要尽可能的探索到状态空间,而其他机器学习已经拥有了足够描述状态空间的数据集。
回想Model-Based Monte-Carl 的思路:估计$T(s, a, s’)$、$Reward(s, a, s’)$,然后使用Value Iteration求解MDP。
Model-Free Monte-Carl提出,既然$T(s, a, s’)$、$Reward(s, a, s’)$ 最后都是为了求$Q_{opt}(s, a)$所用的,那么可以尝试直接估计$Q_{opt}(s, a)$ (无模型指并不尝试构建MDP模型,实际上$Q_{opt}$也可以看作是一个模型)。
在这里插入两个概念:
on-policy: 使用目标策略(target policy)采样得到的样本来进行训练
off-policy:使用行为策略(behavior policy)采样得到的样本进行训练
以on-policy为例,设依据目标策略$ \pi $有如下序列:
则收益为:
\[u_t = r_t + \gamma r_{t+1} + \gamma ^2 r_{t+2} + \dots\]预测$\hat{Q}_{\pi}(s, a)$为从$(s, a)$开始的path们的均值:
\[\hat{Q}_{\pi}(s, a) = \overline{u_t} \ (where\ s_{t-1} = s, a_{t} = a)\]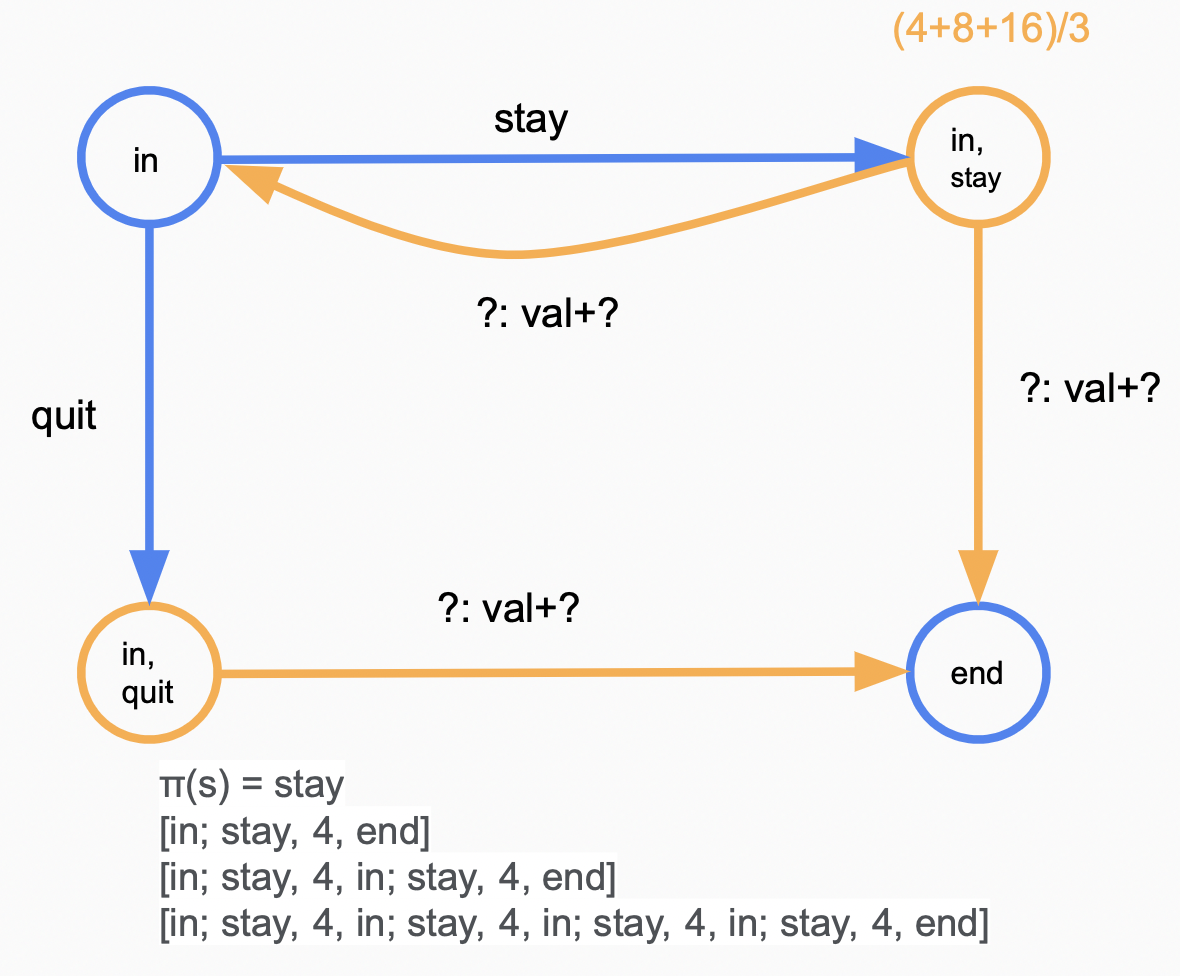
更形式化地来描述求得平均值的过程即为:
${\color[RGB]{159,46,39}{\text{Algorithm: Model-Free Monte-Carl}}}$
\[\begin{align} & on\ each ({\color{Orange}{s,a,u} } ): \notag \\ & \ \ \ \eta = \frac{1}{1 + (\# (s, a)更新次数)} \notag \\ & \ \ \ \hat{Q}_{\pi}(s, a) \gets (1- \eta){\color{red}{\hat{Q}_{\pi}(s, a)}} + \eta {\color{green}{u}} \ \text{(凸组合)} \notag \end{align}\]
实际上这个公式与梯度下降形式非常相像,$\hat{Q}_{\pi}(s, a)$为预测值,$u$为我们试图靠近的target,在接下来的算法中,公式中红色的部分都代表预测值,绿色部分都代表希望靠近的目标值。
\[\hat{Q}_{\pi}(s, a) \gets \hat{Q}_{\pi}(s, a) - \eta[\hat{Q}_{\pi}(s, a) - u]\]Bootstrapping methods
在MC方法中,依赖于完整的回报来更新目标,而Bootstrapping methods根据现有估计更新目标。
SARSA
以SARSA为例 (该名字是因为更新$Q$值过程中使用的序列为$s, a, r, s^{\prime }, a^{\prime }$)。
${\color[RGB]{159,46,39}{\text{Algorithm: SARSA}}}$
\[\begin{align} & on\ each ({\color{Orange}{s, a, r, s^{\prime }, a^{\prime }} } ): \notag \\ & \ \ \ \hat{Q}_{\pi}(s, a) \gets (1- \eta){\color{red}{\hat{Q}_{\pi}(s, a)}} + \eta{\color{green}{[r + \gamma \hat{Q}_{\pi}(s^{\prime }, a^{\prime }) ]}} \notag \end{align}\]
其中,$r$为当前步获得的奖励值,$\hat{Q}_{\pi}(s^{\prime }, a^{\prime })$为算法运行到该步以前的预测值,相较于蒙特卡洛方法,SARSA方法使用了更小的窗口即可完成预测。
举个例子,若已经预测过$\hat{Q}_{\pi}(s, stay) = 11$, 目标策略$\pi(s) = stay$,则有如下计算:
\[\begin{align} & [in; stay, 4, end] & 4 + 0 \notag \\ & [in; stay, 4, in; stay, 4, end] & 4 + 11 \notag \\ & [in; stay, 4, in; stay, 4, in; stay, 4, in; stay, 4, end] & 4 + 11 \notag \end{align}\]Q-learning
目前为止的介绍的方法都是on-policy的 (Model-Free Monte-Carl,SARSA) ,我们遵循一定的策略$\pi$,预测出$\hat{Q}_{\pi}(s, a)$。
Q-learning迈上了off-policy的台阶,直接预测$Q_{opt}(s, a)$ :
${\color[RGB]{159,46,39}{\text{Algorithm: Q-learning [Watkkins/Dayan, 1992]}}}$
\[\begin{align} & on\ each ({\color{Orange}{s, a, r, s^{\prime }} } ): \notag \\ & \ \ \ \hat{Q}_{opt}(s, a) \gets (1- \eta){\color{red}{\hat{Q}_{opt}(s, a)}} + \eta{\color{green}{[r + \gamma \hat{V}_{opt}(s^{\prime })]}} \notag \\ & \ \ \ \hat{V}_{opt}(s^{\prime }) = max_{a^{\prime} \in Action(s^{\prime})} \hat{Q}_{opt}(s^{\prime}, a^{\prime}) \notag \end{align}\]
回顾MDP中的value iteration:
\[Q_{opt}(s, a) = \sum_{s'} T(s, a, s')[{\color{green}{R(s, a, s') + \gamma V_{opt}(s')} }]\]与QL相比,有: $r$ 看作 $R(s, a, s’)$ ,将 $\hat{V_{opt}}(s^{\prime })$ 看作 $V_{opt}(s’)$ ,
并尝试让预测值 $\hat{Q_{opt}}(s, a)$ 不断接近目标值 $r + \gamma \hat{V_{opt}}(s^{\prime })$。
与SARSA相比QL的窗口不包含下一步$a^{\prime}$,因为我们并不是遵循一定的策略选择下一步的动作,而是贪心的选择收益最大的动作。
epsilon-greedy policy
在Monte-Carlo methods一节中提到,强化学习的探索是十分重要的:我们希望尽可能的探索状态空间,同时希望利用现有的探索信息得到高回报。$\varepsilon \text{-greedy}$ 尝试在“保持最优”和”随机探索”之间找到平衡:
${\color[RGB]{159,46,39}{\text{Algorithm: epsilon-greedy policy}}}$
\[\pi_{act}(s) = \begin{cases} argmax_{a\in Actions}\hat{Q}_{opt}(s, a) & \text{ probability } 1-\varepsilon \notag \\ \text{random from }Action(s) & \text{ probability } \varepsilon \notag \end{cases}\]
其中$\pi_{act}(s)$指我们遵循的搜索策略。
Deep Q-Network
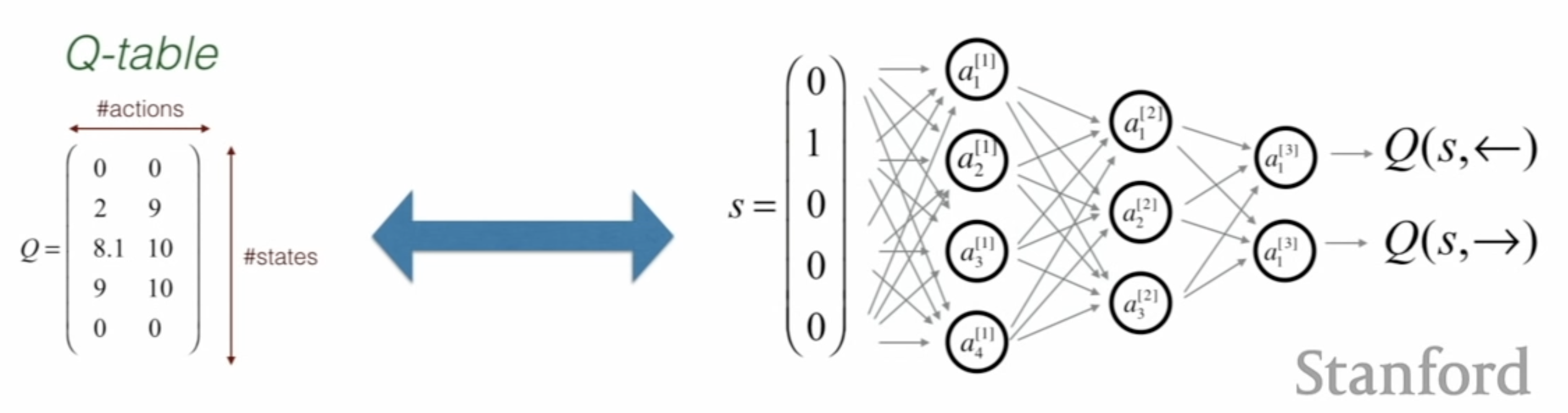
在Q-learning中,为了获得$Q^∗(⋅)$ (最优的$Q_{opt}$),我们需要使用一个 $[size(States), size(Actions)]$ 的$Q-Table$ 将所有状态行为对保存起来。当状态和行为空间非常大的时候,全部存储下来几乎不可行。在这种情况下,人们提出使用函数来近似$Q$值,这个方法被称作函数拟合,即寻找一个$Q\text{-}function$,替代原来的$Q-Table$的作用。我认为这可以看作是一个“用时间换空间”的想法,当然$Q\text{-}function$的作用不止于此,它为我们提供了更多特征提取及与强化学习与机器学习结合的可能。
在这种情况下,另$\hat{Q_{opt}}(s, a;\mathbf{w}) = \mathbf{w} \cdot \phi (s,a)$ (粗体符号代表向量),$\mathbf{w}$代表权重向量,$\phi (s,a)$代表特征值向量。如在赌钱游戏中,我们可以定义$\phi_{1}(s,a) = 1$代表$[a =stay ]$,用$\phi_{2}(s,a)$代表$[s = in ] $……以此类推。
${\color[RGB]{159,46,39}{\text{Algorithm: Q-learning with function approximation}}}$
\[\begin{align} & on\ each ( {\color{Orange}{s, a, r, s^{\prime }} } ): \notag \\ & \ \ \ \mathbf{w} \gets \mathbf{w} - \eta[{\color{red}{\hat{Q}_{opt}(s, a, \mathbf{w})}} - {\color{green}{(r + \gamma \hat{V}_{opt}(s^{\prime }))}}]\phi (s,a) \notag \end{align}\]
可以将$\hat{Q_{opt}}(s, a, \mathbf{w}) - (r + \gamma \hat{V_{opt}}(s^{\prime }))$视作计算残差,$\phi (s,a)$帮助我们将属于$\hat{Q_{opt}}(s, a, \mathbf{w})$的残差宽度拓展到$\mathbf{w}$,$\eta$为步长。
通常使用深度学习模型模拟$Q$值,我们称之为$Q\text{-}network$。以一个经典Atari游戏Breakout为例 (图源自Stanford公开课1):
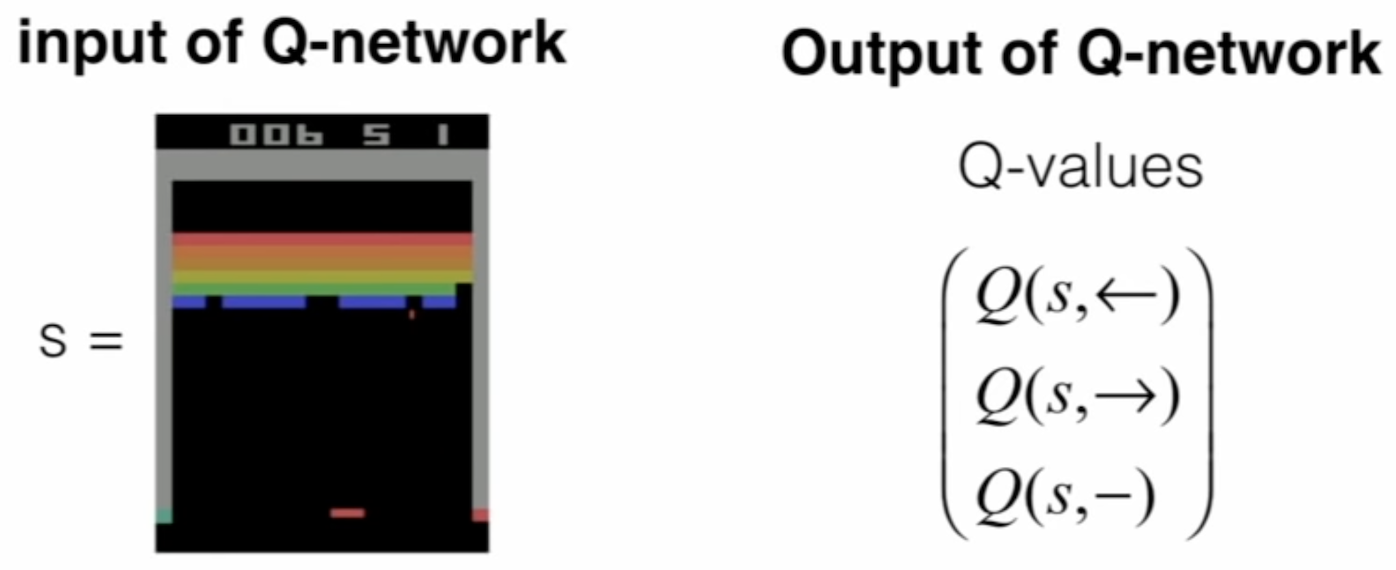
在此学习任务中,我们的目标是用一个小球消除所有的彩色砖块,以预处理过的像素 (如转换为灰度值图像,图像裁剪,合并连续几帧作为一次输入)作为输入,经过$Q\text{-}network$得到各特征值,
算法粗略的伪代码如下:
初始化Q-network:
for each epoch:
从初态s开始
for each time-step:
另s在Q-network中前向传播,获得a (argmax(Q(s,a)))
选择动作a,得到r及新状态s'
s'在Q-network中前向传播,计算target: y
依据梯度下降更新网络参数
考虑我们会遇到的问题,假设某一步我们希望代理执行小木板左移,定义loss如下:
\[L = (y - Q(s, ⬅)) \\ y = r_{⬅} + \gamma \ max_{a^{\prime}}(Q(s_{⬅}^{next}, a^{\prime}))\]首先,我们的”标签值”并不是固定的 (在每轮迭代中, $Q\text{-}network$的更新使得$Q(s_{⬅}^{next}, a^{\prime})$也在不断变化),在反向传播的过程中,如果尝试计算$L$对$Q$的偏导数将得到一个循环算式,网络无法稳定下来。
其次,监督学习拥有一个完备的数据集, 在多个epoch中,将会重复访问数据epoch次,但回想提到过的强化学习的”探索“,强化学习在“探索”获得数据的同时进行训练,我们可能只会访问某些状态一次,甚至访问不到该状态。
另外,如果按照探索序列的顺序进行训练,连续数据点之间会有许多相关性。如果你拥有一个分类猫与狗的CNN分类器,并在一段时间内全部提供猫的数据集对CNN进行训练,下一段时间内全投递狗的数据集,可想而知该分类器在尝试狗的数据集时会有极大的猫偏向性。 $Q\text{-}network$同理,以上文提到的Atari游戏Breakout为例,小球在一段时间内可能连续上升或连续下降,在该段时间内网络将被期望做出连续左移或连续右移的动作,这种连续性为训练带来了困难。
Deep Q-Network2 (Mnih el. 2015)在解决上述问题上作出了突出贡献,研究人员提出了两个创新机制:
- 经验重放 (Experience Replay):每一步数据$E_t=(s_t, a_t, r_t, s_{t+1})$被存储在一个重放缓冲区$D_t={e_1, \dots, e_t}$中($D_t$中会包含许多轮数据)。在Q-learning的更新阶段,样本从回放缓冲区中随机采样出来,每个样本都可以被使用很多次。经验回放可以改善数据效率,消除所观察到序列间的相关性,并且平滑数据分布的变化。
- 阶段目标更新 (Periodically Update Target):$Q$值的优化目标是周期性更新的,网$Q\text{-}network$络每$C$步都会被复制并冻结作为优化目标。阶段目标更新克服了短期震荡问题,可以让训练更加稳定。
损失函数定义为:
\[\mathcal{L}(\theta) = \mathbb{E}_{(s, a, r, s') \sim U(D)} \Big[ \big( r + \gamma \max_{a'} Q(s', a'; \theta^{-}) - Q(s, a; \theta) \big)^2 \Big]\]其中,$(s, a, r, s’) \sim U(D)$表示从缓存$D$中均匀随机抽取的样本。$\theta^{-}$为被冻结网络的参数,$\mathbb{E}$代表对一个batch的数据计算期望损失,即一个 batch中各数据损失的均值。
算法的伪代码描述如下:

对DQN的优化如double DQN等,待补充
Policy Gradient
由于本节所使用的数学符号,含义有些变化,对于可能造成歧义的部分符号,在此说明
| Symbol | Meaning |
|---|---|
| $V(s)$ | 从状态$s$开始的收益函数 |
| $Q(s,a)$ | 从概率节点$(s, a)$开始的收益函数 |
| $\theta $ | 待训练的模型参数 |
| $\pi(a \vert s)$ | $s$状态做出动作$a$的概率 |
| $\mathbb{P}$ / $P$ | 概率 |
| $\mathbb{E}$ | 期望 |
| $\nabla$ | 偏导数 |
| $\Delta $ | 梯度 |
| $\alpha$ | 学习率,也叫步长 |
| $J$ | 目标函数 |
| $\tau $ | 轨迹 $(s_0, a_0, r_0,\dots, s_{T-1}, a_{T-1}, r_{T-1}, s_T)$ |
| $R(\tau )$ | 轨迹的收益总和 |
| $\alpha$ | 学习率,也叫步长 |
stochastic policy
目前,我们提到的算法都是value-based 算法:我们尝试将 $V_\theta (s)$ 或 $Q_\theta (s,a)$ 最大化,并从中提取出最后的策略。policy-based提出我们可以尝试直接学习最终策略。此外,在此之前我们提到的策略皆为确定性策略,即$\pi (s) = a$,确定性策略在某些场景将遇到瓶颈。随机策略指我们的策略是遵循一定概率发生的:$\pi(a \vert s) = \mathbb{P}_\pi [A=a \vert S=s]$
objective functions
基于策略的算法希望找到最大化收益的随机策略$\pi_\theta (a \vert s)$的$\theta $,有几下几种目标函数。
在离散空间内:
\[J_1(\theta) = V^{\pi_\theta}(s_1) = \mathbb{E}_{\pi_\theta}[v_1]\]在连续空间,目标函数可以定义为策略的均值 (average value) 或在一步动作的均值 (average reward):
\[J_{avV}(\theta) = \sum_{s} d^{\pi_\theta}(s) V^{\pi_\theta}(s) = \sum_{s} \Big( d^{\pi_\theta}(s) \sum_{a} \pi_\theta (a \vert s) Q^\pi(s, a) \Big) \\ J_{avR}(\theta) = \sum_{s} \Big( d^{\pi_\theta}(s) \sum_{a} \pi_\theta (a \vert s) R(s, a) \Big)\]其中,$d^{\pi_\theta}(s)$ 为$\pi_\theta$所决定的马尔可夫链的平稳分布。在接下来的内容主要讨论离散空间的情况。
computing the gradient
为了使用梯度下降法对目标函数求最优,首先计算代优化参数$\theta $的梯度。
\[\Delta \theta = \alpha \nabla_\theta J(\theta)\]考虑如何计算偏导数,离散空间下,设目标函数为
\[J(\theta) = \mathbb{E}_{\tau ~ \pi_\theta}[R(\theta)] = \sum_{\tau}P(\tau;\theta)R(\tau)\]其中$\tau$指从初始状态开始的轨迹,$P$代表随机策略$\pi$下改轨迹出现的概率,$R$代表轨迹总收益。
\[\begin{align} \nabla_\theta J(\theta) &= \nabla_\theta \sum_{\tau}P(\tau;\theta)R(\tau) \\ &= \sum_{\tau} \nabla_\theta P(\tau;\theta)R(\tau) \\ &= \sum_{\tau} \frac{P(\tau;\theta)}{P(\tau;\theta)} \nabla_\theta P(\tau;\theta)R(\tau) \\ &= \sum_{\tau} P(\tau;\theta)R(\tau) \frac{\nabla_\theta P(\tau;\theta)}{P(\tau;\theta)} \\ &= \sum_{\tau} P(\tau;\theta)R(\tau) \nabla_\theta \text{ log } P(\tau;\theta) \\ &= \mathbb{E}_{\tau ~ \pi_\theta}[R(\tau) \nabla_\theta \text{ log } P(\tau;\theta)] \end{align}\]其中,$(4)$式中的 $\frac{P(\tau;\theta)}{P(\tau;\theta)}$ 称作似然比 (likelihood ratio),我们此刻有
计算$\nabla_\theta \text{ log } P(\tau;\theta)$,将轨迹$\tau $分解为$s$及$a$,在$(8)$式实现了动态模型与策略的解耦合 (动态模型指 $(s_t, a_t)$转移到$s_{t+1}$的概率由环境决定,与策略无关);最终求导时,初态分布,动态模型都将求导得到零,我们将得到一个优美的公式:
\[\begin{align} \nabla_\theta \text{ log } P(\tau;\theta) &= \nabla_\theta log \Big[ \underbrace{\mu(s_0)}_{初态分布} \prod_{t=0}^{T-1} \underbrace{ \pi_\theta(a_t|s_t)}_{策略}\ \underbrace{P(s_{t+1}|s_t, a_t) }_{动态模型} \Big] \\ &= \nabla_\theta \Big[ \text{ log }\mu(s_0) + \sum_{t=0}^{T-1}\text{ log }\pi_\theta(a_t|s_t) + \text{ log } P(s_{t+1}|s_t, a_t) \Big] \\ &= \sum_{t=0}^{T-1} \nabla_\theta \text{ log }\pi_\theta(a_t|s_t) \end{align}\]其中,$\text{ log }\pi_\theta(a_t|s_t)$称作score function;
$(9)$代入$(6)$得
感谢log,我们目前的score function经过解耦合,仅仅与策略本身有关。
policy gradient theorem
策略梯度定理概括了似然比方法:
${\color[RGB]{159,46,39}{\text{Policy Gradient Theorem}}}$
对于任意可微策略函数 $\pi_\theta (s,a)$,
对任意目标函数 $J = J_1, J_{avR}, \frac{1}{1 - \gamma} J_{avV}$,
策略梯度为:
\[\nabla_\theta J(\theta) = \mathbb{E}_{\pi_\theta}[\nabla_\theta \text{ log }\pi_\theta (s,a) Q^{\pi_\theta}(s,a)]\]
关于定理详细可看此书13.1章。
use temporal structure
目前我们的梯度计算需要一个完整的轨迹,回顾之前的TD方法,我们希望可以每一时刻更新梯度。
回顾之前得到的:
\[\nabla_\theta J(\theta) = \nabla_\theta \mathbb{E}_{\tau ~ \pi_\theta}[R(\tau)] = \mathbb{E}_{\tau ~ \pi_\theta} \Big[R(\tau) \sum_{t=0}^{T-1} \nabla_\theta \text{ log }\pi_\theta(a_t|s_t) \Big]\]其中
\[R(\tau) = \sum_{t=0}^{T-1} R(s_t, a_t)\]我们可以用相同的推导过程将关于$R(\tau)$的公式推导到单步奖励上:
\[\nabla_\theta \mathbb{E}_{\tau ~ \pi_\theta}[r_{t^{\prime}}] = \mathbb{E}_{\pi_\theta} \Big[r_{t^{\prime}} \sum_{t=0}^{t^{\prime}} \nabla_\theta \text{ log }\pi_\theta(a_t|s_t) \Big]\]由 $\sum_{t=t^{\prime}}^{T-1}r_{t^{\prime}}^{(i)} = G_t^{(i)}$,代表我们对$Q$的一种近似估计,得到如下式子
\[\begin{align} \nabla_\theta J(\theta) = \nabla_\theta \mathbb{E}_{\tau ~ \pi_\theta}[R(\tau)] &= \mathbb{E}_{\pi_\theta} \Big[ \sum_{t=0}^{T-1}r_{t^{\prime}} \sum_{t=0}^{t^{\prime}} \nabla_\theta \text{ log }\pi_\theta(a_t|s_t) \Big] \notag \\ &= \mathbb{E}_{\pi_\theta} \Big[\sum_{t=0}^{T-1} \nabla_\theta \text{ log }\pi_\theta(a_t|s_t) \sum_{t^{\prime} = t}^{T-1} r_{t^{\prime}} \Big] \notag \\ &= \mathbb{E}_{\pi_\theta} \Big[\sum_{t=0}^{T-1}G_t \cdot \nabla_\theta \text{ log }\pi_\theta(a_t|s_t) \Big] \notag \\ & \approx \frac{1}{m} \sum_{i=1}^{m} \sum_{t=0}^{T-1}G_t^{(i)} \cdot \nabla_\theta \text{ log }\pi_\theta(a_t^{(i)}|s_t^{(i)}) \notag \end{align}\]如此一来,$\theta \gets \theta + \alpha \nabla_\theta J(\theta)$经过推导,可在每一时刻进行梯度更新。 \(\theta \gets \theta + \alpha \cdot G_t \nabla_\theta \text{ log}\pi_\theta(a_t|s_t)\)
REINFORCE: Monte-Carlo Policy Gradient
${\color[RGB]{159,46,39}{\text{Algorithm: REINFORCE}}}$
初始化策略模型参数$\theta$
\[\begin{align} & \text{for each }(s_0, a_0, r_0,\dots, s_{T-1}, a_{T-1}, r_{T-1}, s_T)~\pi_\theta : \notag \\ & \ \ \ \ \text{for }t=1 \text{ to }T-1:\notag \\ &\ \ \ \ \ \ \ \ \theta \gets \theta + \alpha \cdot G_t \nabla_\theta \text{ log}\pi_\theta(a_t|s_t) \notag \\ & \ \ \ \ \text{return }\theta \notag \end{align}\]
parametric policy
为了描述策略,对策略进行参数化,在离散空间可用softmax:
其中 $\phi$代表特征函数,$\theta$代表参数。
连续空间常用高斯分布:$a \sim \mathcal{N}(\mu(s), \sigma^2) $,其中均值是特征值的线性组合 $\mu(s) = \phi(s)^T \theta$,$\sigma^2$可以是固定的也可以作为待优参数的一部分。
Variance reduction with a baseline
观察目前的Monte-Carlo梯度更新策略
\[\theta \gets \theta + \alpha \cdot G_t \nabla_\theta \text{ log}\pi_\theta(a_t|s_t) \notag\]我们用$ G_t $代替了$Q_t$ ,但这种做法存在着一些问题:
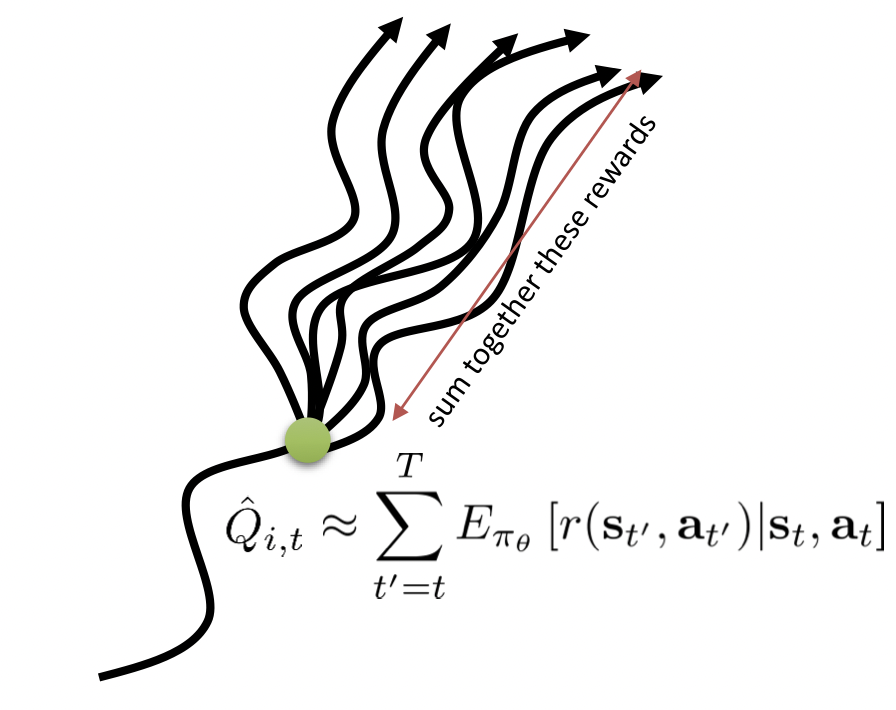
(图源自CS 294-112: Deep Reinforcement Learning. Sergey Levine)
在状态$s$ (图中绿色点)时,可能的轨迹有多条,这些轨迹求得的期望才是$Q$值;目前我们仅使用一条轨迹的$\sum_{t=t^{\prime}}^{T-1}r_{t^{\prime}}^{(i)} = G_t^{(i)}$代替,这带来了高方差;一种方法是增加基线$b(s)$,通常取值为目前所有轨迹价值的平均值。
\[\nabla_\theta J(\theta) = \nabla_\theta \mathbb{E}_{\tau ~ \pi_\theta}[R(\tau)] = \mathbb{E}_{\pi_\theta} \Big[\sum_{t=0}^{T-1}(G_t - b(s_t)) \cdot \nabla_\theta \text{ log }\pi_\theta(a_t|s_t) \Big]\]其中$(G_t - b(s_t))$常称为优势函数 $A_t$ ,他评估了动作$a_t$的优劣。直观来讲,如果当前轨迹的$G_t$大于均值,则$G_t-b(s_t)>0$,上式将增加他的log-概率,否则优势函数小于0,上式将减小他的log-概率;
推导可得 \(\mathbb{E}_{\tau}[b(s_t) \nabla_\theta \text{ log }\pi_\theta(a_t|s_t)] = 0\) 所以用$A_t$代替$G_t$后依然是无偏的。
${\color[RGB]{159,46,39}{\text{Algorithm: Vanilla Policy Gradient}}}$
初始化策略模型参数$\theta$及基线$b(s)$,e.g. 0,设$b(s)$的参数为$\mathbf{w}$
\[\begin{align} & \text{for iteration}=1,2,\dots: \notag \\ & \ \ \ \ \text{根据当前策略} \pi_{\theta}计算m个轨迹的集合 \notag \\ & \ \ \ \ \text{for each time step }t \text{ of each trajectory }\tau^{i}:\notag \\ &\ \ \ \ \ \ \ \ G_t^{(i)} = \sum_{t^{\prime} = t}^{T-1} r_{t^{\prime}} \notag \\ &\ \ \ \ \ \ \ \ \hat{A}_t^{(i)} = G_t^{(i)} - b(s_t)\notag \\ & \ \ \ \ \text{更新}\mathbf{w}(最小化 \sum_{i=1}^{m}\sum_{t=0}^{T-1} \left \| b(s_t)-G_t^{(i)} \right \| ^2 ) \notag \\ & \ \ \ \ \text{更新}\theta :\hat{g} = \sum_{i=1}^{m} \sum_{t=0}^{T-1} \hat{A}_t^{(i)} \nabla_\theta \text{ log }\pi_\theta(a_t^{(i)}|s_t^{(i)}),使用SGD(\theta \gets \theta + \alpha \cdot \hat{g})、Adam等更新 \notag \\ &\text{return }\theta \text{ 及 }b(s) \notag \end{align}\]
Actor-Critic
接下来从MDP开始重新快速回顾一下我们是如何走到这一步的。
首先介绍了MDP过程以及解决MDP过程的两种方法:求$V_\pi、Q_\pi$的policy evaluation方法及求最优价值$V_{opt}、Q_{opt}$的value iteration方法;
紧接着提出了RL过程,与MDP不同的是我们不知道$(s,a)$的转移概率和回报,借鉴MDP的解决方案,人们出了可以使用探索序列构造MDP模型,然后用MDP的方法求解,紧接着发现可以直接估计价值函数 (轨迹收益的均值),于是就有了Model-Free Monte-Carl方法;
在这里人们发现探索序列对估计结果有很大的影响,介绍了一种随机探索方案epsilon-greedy policy;
由于在蒙卡洛特方法中更新梯度需要完整的轨迹,TD方法提出可以在更新时使用现有的估计$\hat{Q}$,在这里提到了SARSA方法;Q-learing方法提供了off-policy的方法,DQN是对Q-learning的改进,我们并不需要储存现有的$\hat{Q}$,而是使用另一个网络拟合它,DQN还提出了经验重放和冻结网络这两种改进思路;
以上均称之为value-based方法,因为我们尝试的是学习价值函数,提取出最后的策略,policy-based方法尝试直接学习策略,在这里经过计算最后得到一种可以在每时刻进行更新的REINFORCE方法;该方法存在高方差的主要原因是我们使用单轨迹代替了轨迹的期望 (可能的轨迹有多条),基于此人们提出了基线方法进行修正,即 Vanilla Policy Gradient方法,但是由于引入了基线,我们在更新的时候又不得不使用完整的轨迹。
Actor-Critic方法,可以看作是对改善REINFORCE高方差的另一尝试,改进思路类似DQN:既然高方差是对$Q$的不当替换带来的,我们用另一个网络学习$Q$,使用TD方法既可以在不使用完整轨迹的情况下更新网络;其中,Actor指导着动作,Critic代表对价值的评估。
${\color[RGB]{159,46,39}{\text{Algorithm: Action-Value Actor-Critic}}}$3
$Q_w(s, a) = \phi(s, a)^Tw$,学习率$\alpha 、\beta $,衰减率$\gamma $
Critic:模拟$Q_w$,参数$w$
Actor:模拟$\pi_\theta $,参数$\theta $
初始化初始状态$s$,网络参数$\theta $,使用Actor得到$a \sim \pi_{\theta}$
\[\begin{align} & \text{for each time step}: \notag \\ & \ \ \ \ 基于s, a得到 r \sim R_s^a,s^{\prime} \sim P_s^a \notag \\ & \ \ \ \ 使用Actor得到a^{\prime} \sim \pi_{\theta}(s^{\prime},a^{\prime}) \notag \\ & \ \ \ \ 使用Critic得到 Q_w(s, a),Q_w(s^{\prime},a^{\prime}) \notag \\ & \ \ \ \ 计算TD误差,稍后将用于更新Critic:\ \ \delta = r + \gamma Q_w(s^{\prime},a^{\prime}) - Q_w(s, a) \notag \\ & \ \ \ \ 更新Actor:\ \ \theta = \theta + \alpha \nabla_\theta \text{ log }\pi_\theta(s, a) Q_w(s, a) \notag \\ & \ \ \ \ 更新Critic:\ \ w \gets w + \beta \ \delta \ \phi(s, a) \notag \\ & \ \ \ \ 获得下一个状态及动作\ \ a \gets a^{\prime},\ s \gets s^{\prime} \notag \end{align}\]
关于Actor-Critic的改进,有两个经典算法,一个是DDPG算法,使用了双Actor神经网络和双Critic神经网络的方法来改善收敛性。另一个是A3C算法,使用了多线程的方式,一个主线程负责更新Actor和Critic的参数,多个辅线程负责分别和环境交互,得到梯度更新值,汇总更新主线程的参数。而所有的辅线程会定期从主线程更新网络参数。这些辅线程起到了类似DQN中经验回放的作用,但是效果更好。
-
Stanford CS221: AI (Autumn 2019) by Stanford University on YouTube. ↩︎
-
Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning[J]. nature, 2015, 518(7540): 529-533. ↩︎
-
Reinforcement Learning lectures by David Silver on YouTube. ↩︎